Graph f(x) = −2x 2 3x – 3 a = −2, so the graph will open down and be thinner than f(x) = x 2 c = −3, so it will move to intercept the yaxis at (0, −3) Before making a table of values, look at the values of a and c to get a general idea of what the graph should look likeExplain This problem has been solved!Then the graph of y = f(x c) is obtained by translating the graph of y = f(x) c units to the right;
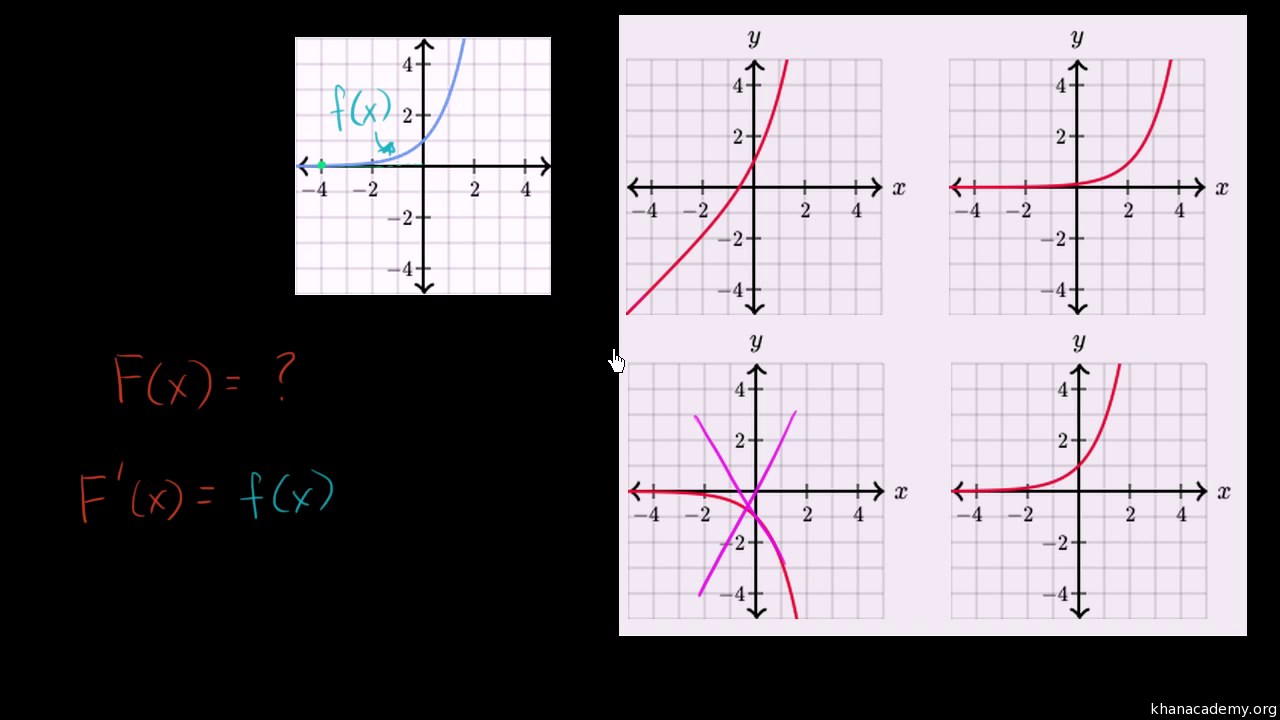
Visually Determining Antiderivative Video Khan Academy
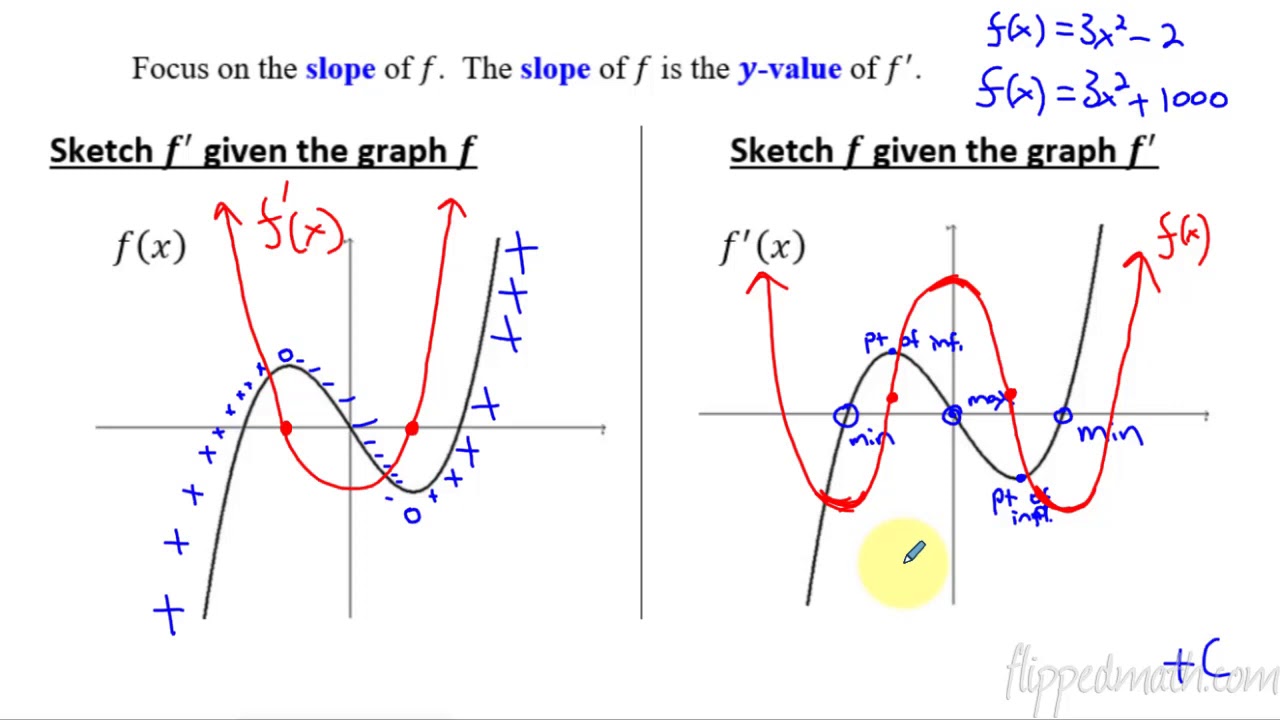
How to read f'(x)
How to read f'(x)- · How does the graph of g(x) = 3X – 2 compare to the graph of f(x) = 3X? · the figure shows the graph of F', the derivative of a function f the domain of the function f is the set of all X such that 3 or equal to x Math compare the parent function f(x)=x^2 to the quadractic function f(x)=2x^26 the 6 in the function does which of the following?
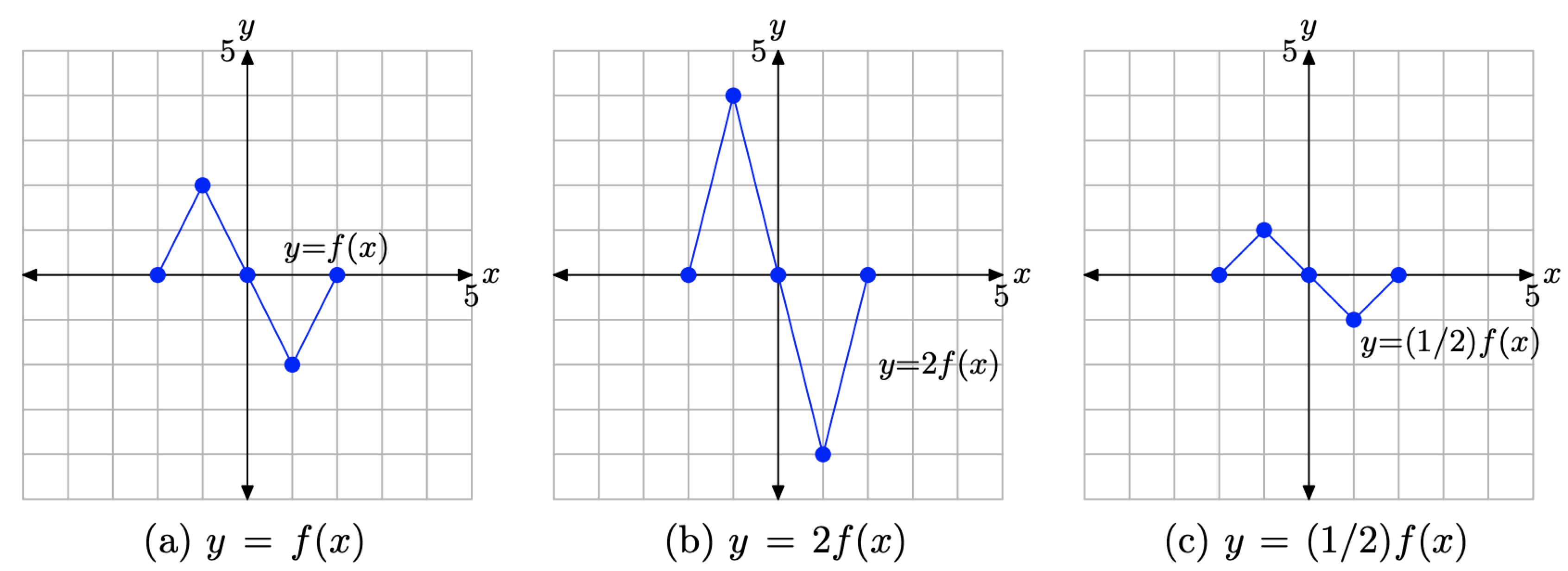



2 5 Vertical Transformations Mathematics Libretexts
· In two or more complete sentences, compare the number of xintercepts in the graph of f(x)=x^2 to the number of xintercepts in the graph of g(x)=x^25 Be sure to include the transformations that occurred between the parent function f(x) and its image g(x)Compare the functions f(x)=x^{10} and g(x)=e^{x} by graph ing both f and g in several viewing rectangles When does the graph of g finally surpass the graph o 🚨 Hurry, space in our FREE summer bootcamps is running out 🚨 Claim your spot hereTranslations of Functions Suppose that y = f(x) is a function and c > 0;
Algebra 2 Answers Serena D Apr 29, 18 C Explanation It has been shifted down #4# units and to the left #8# units #f(x)=sqrt(xaVideo Transcript {'transcript' "we have to function by Required to express y Z minus bicycle Expert is fading function It's crop is like this No, you see disfunction That is a negative sign So the draft will be reflected around the X axis So this is going to bicycle minus X squaredF(x) means that you replace every 'x' by x f(x) means that you change or of f(x) It is the same function, if the function only has x with odd exponents like x, x^3, x^5, x^(7) etc However, if you have anyhing else, f(x) is not f(x) F
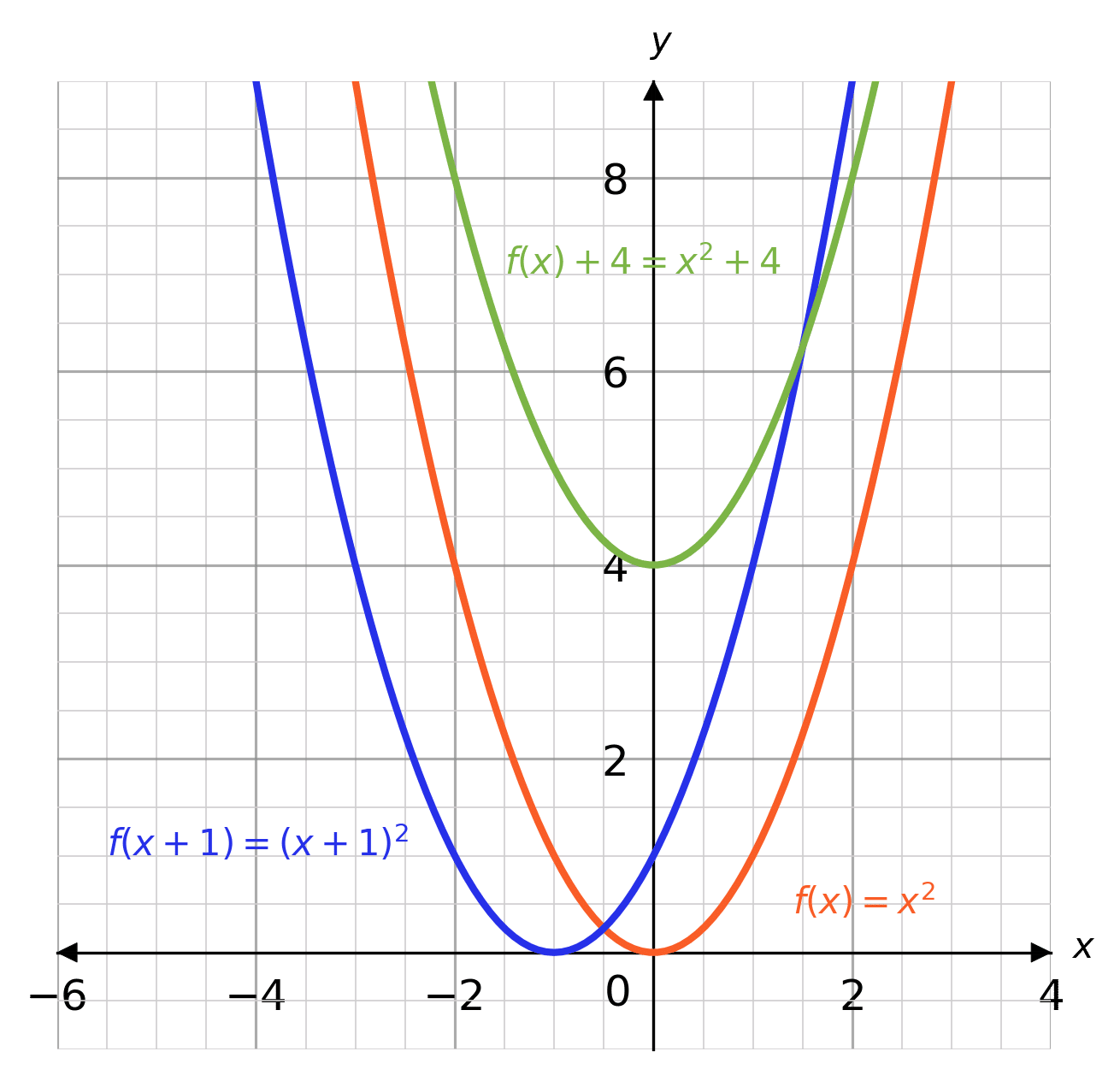
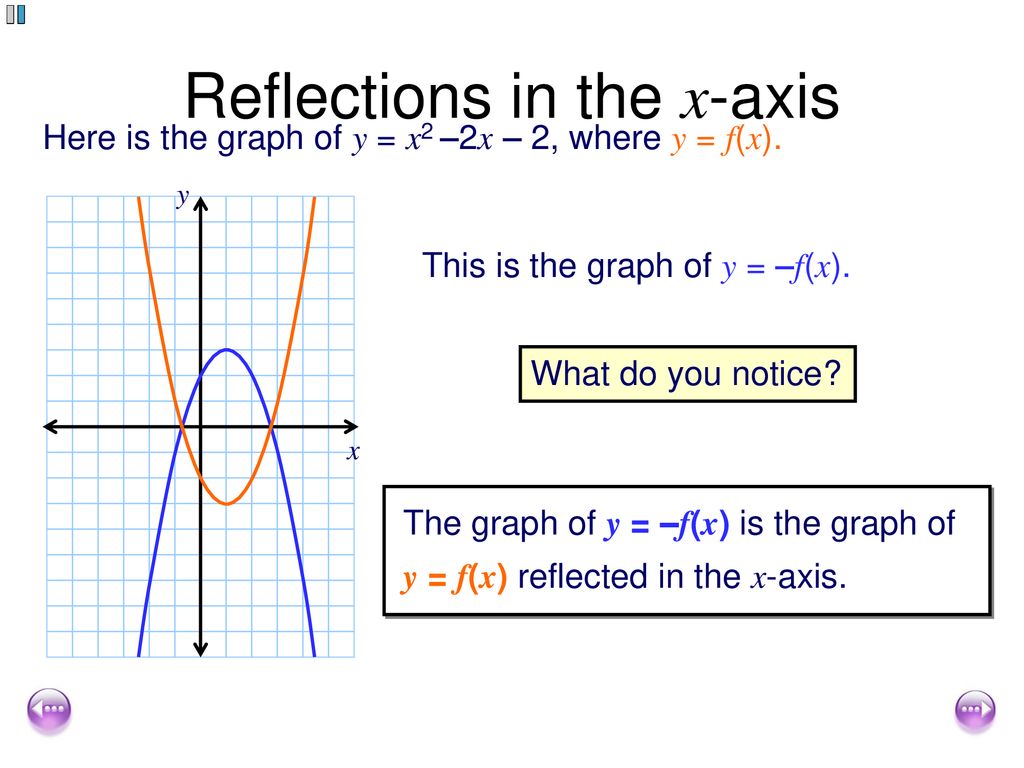
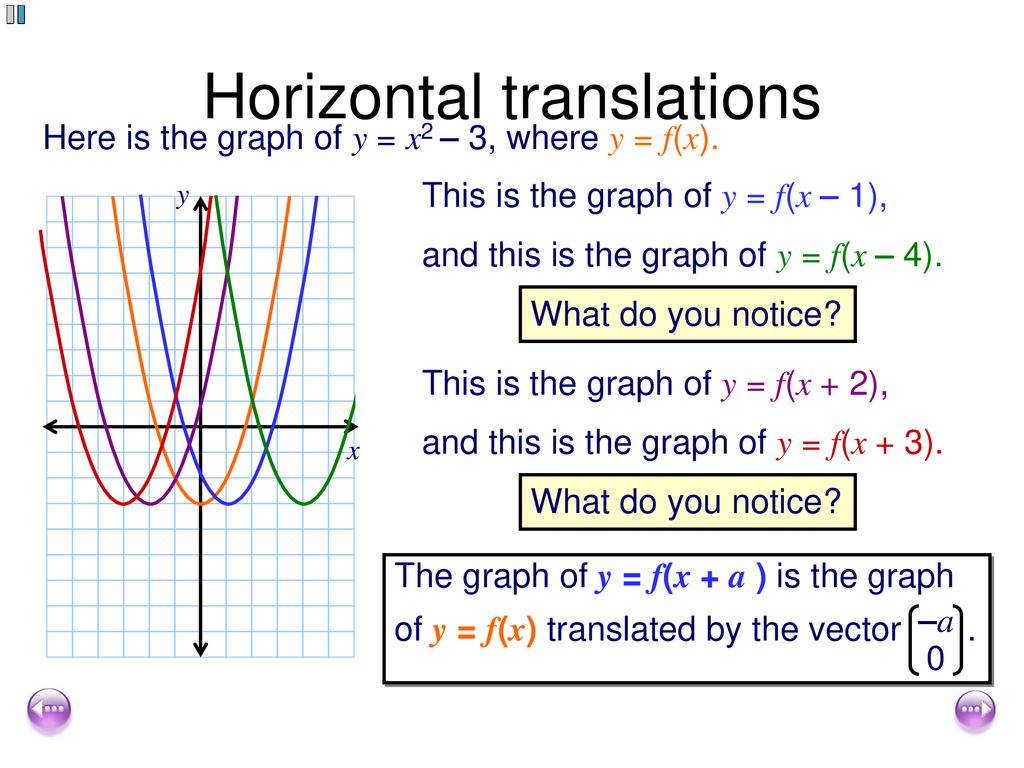
Functions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and images (y = f(xThat is, the rule for this transformation is –f (x) To see how this works, take a look at the graph of h(x) = x 2 2x – 3The graph of y = f(x) c is obtained by translating the graph of y = f(x) c units upwards;
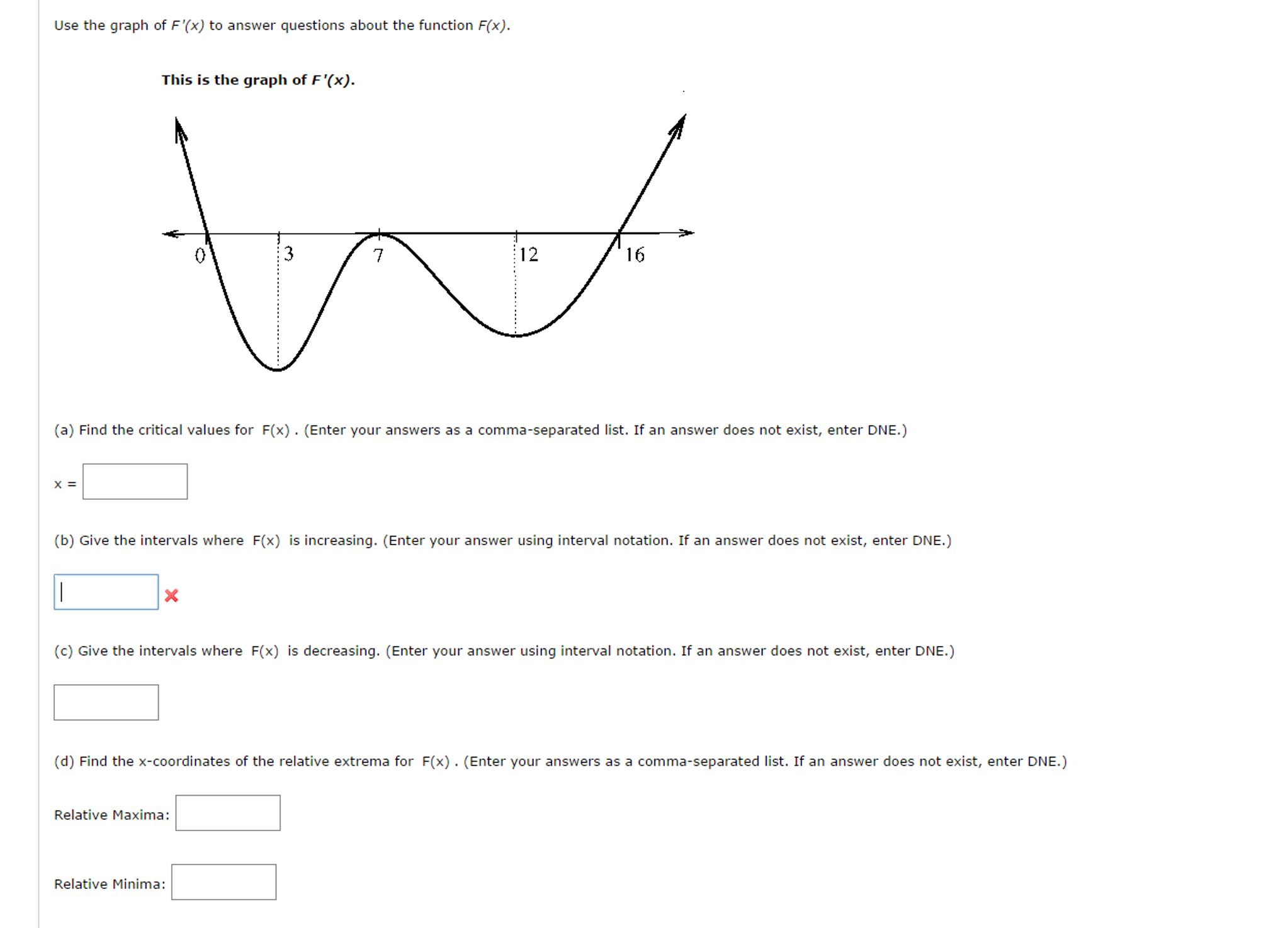



Solved Use The Graph Of F X To Answer Questions About T Chegg Com
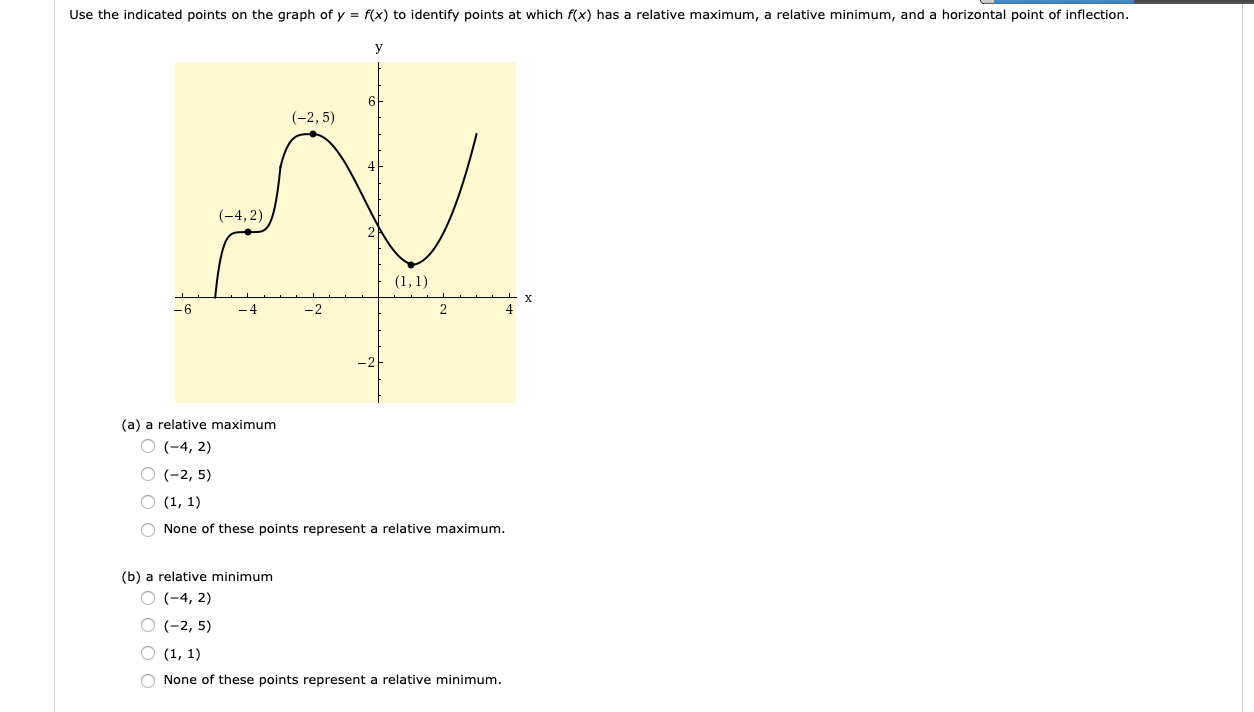



Solved Use The Indicated Points On The Graph Of Y F X Chegg Com
SubsectionVertical Shifts Figure232 shows the graphs of f(x) = x2 4, f ( x) = x 2 4, g(x) = x2 − 4, g ( x) = x 2 − 4, and the basic parabola, y = x2 By comparing tables of values, we can see exactly how the graphs of f and g are related to the basic parabolaWhat effect will f(x a) have on the graph of f(x)?Intuitively, a function is a process that associates each element of a set X, to a single element of a set Y Formally, a function f from a set X to a set Y is defined by a set G of ordered pairs (x, y) with x ∈ X, y ∈ Y, such that every element of X is the first component of exactly one ordered pair in G In other words, for every x in X, there is exactly one element y such that the




Using Transformations To Graph Functions



Graph Transformations Worksheets Questions And Revision Mme
The graph of y = f(x c) is obtained by translating the graph of y = f(x) c units to the left;Question 31 SURVEY 30 seconds Q Quadratic function f (x)=x2 is graphed on a coordinate plane The graph of a new quadratic is formed by changing the vertex to (3, 0) Which function could represent the new quadratic?Answer choices g (x) = x2 3 g (x) = (x 3) 2



Solved This Is The Graph Of F X 15 A Find The Critica Chegg Com
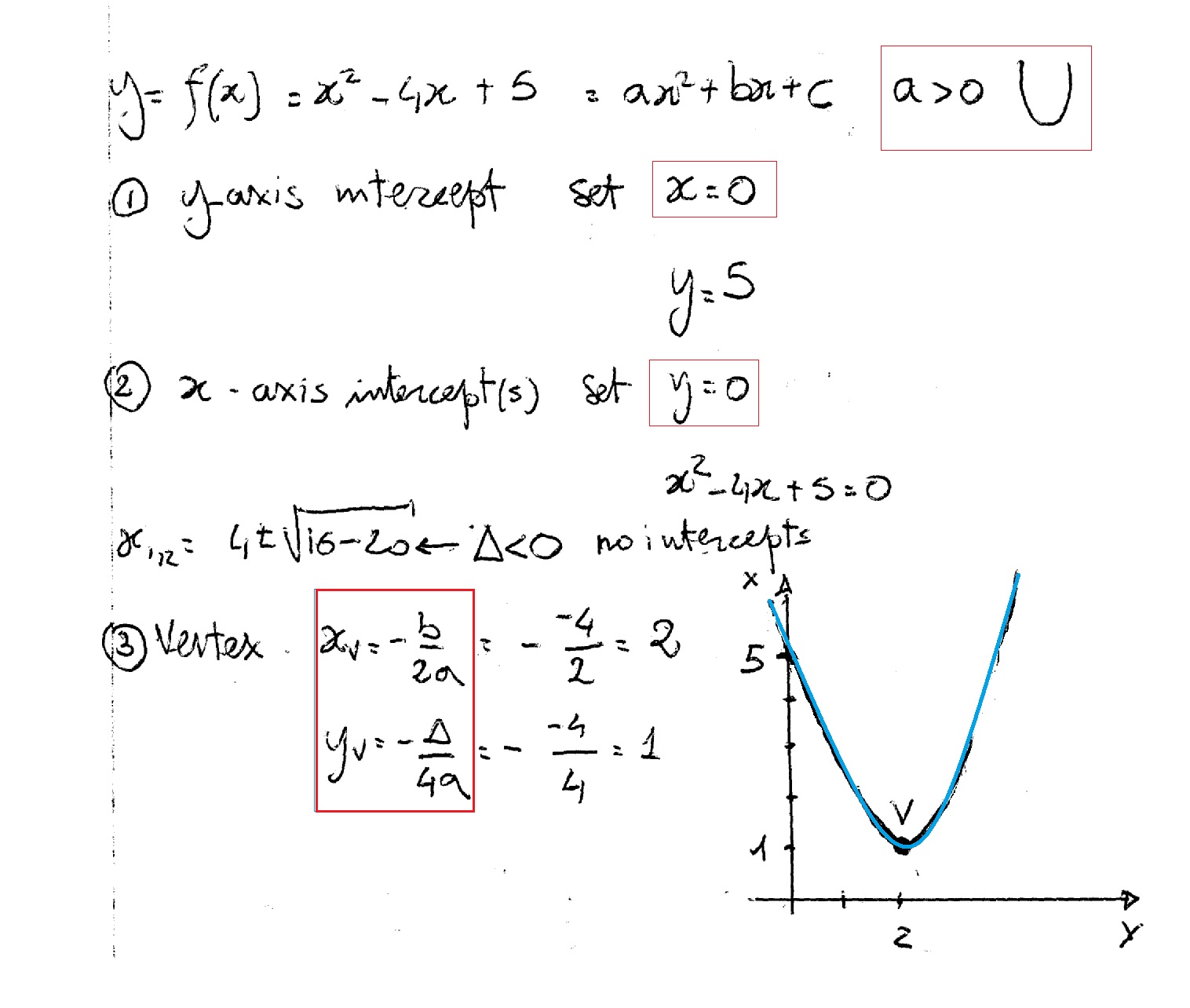



How Do You Graph F X X 2 4x 5 Socratic
Graphs of trigonometric functions The graph of the cosine function f ( x) = cos x To draw the graph of the cosine function divide the unit circle and x axis of a Cartesian coordinate system the same way as when drawing the sine function The abscissas of the ending points of arcs x, of the unit circle, are now the ordinates of theDraw the graph of f(x) = (x − 2) 2 − 1 (or f(x) = x 2 − 4x 3) and compare it to the basic graph g(x) = x 2 If we use the same method as in the previous example we can guess that the graph has moved two units to the right and one unit down Now we will check this by making a table of values, beginning with x = 0 and drawing the graphFor each x x value, there is one y y value Select few x x values from the domain It would be more useful to select the values so that they are around the x x value of the absolute value vertex Tap for more steps Substitute the x x value − 2 2 into f ( x) = x f ( x) = x



4 3 Using Derivatives For Curve Sketching Ppt Download



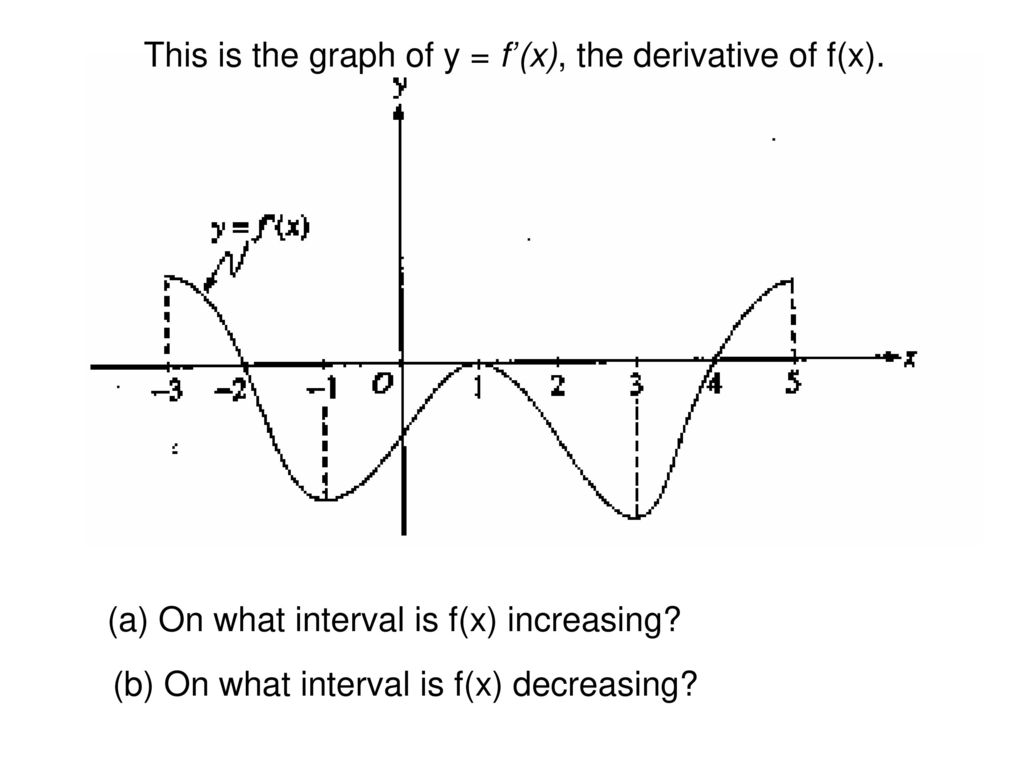
5 8 Sketching Graphs Of Functions And Their Derivatives Calculus
Ait makes the graph narrower than the parent function bit makes the graph wider than the parentThe graph of the function f (x) is shown belowAccording to this graph we havef'a is (positive, equal to zero, or negative)f'b is (positive, equal to zero, or negative)f'c is (positive, equal to zero, or negative)The parameter a can be added to or subtracted from the input x before the rule f is applied y = f(x) becomes y = f(x ± a) These transformations are called horizontal shifts or translationsThey move the graph of the given function left (adding positive a) or right (subtracting positive a)
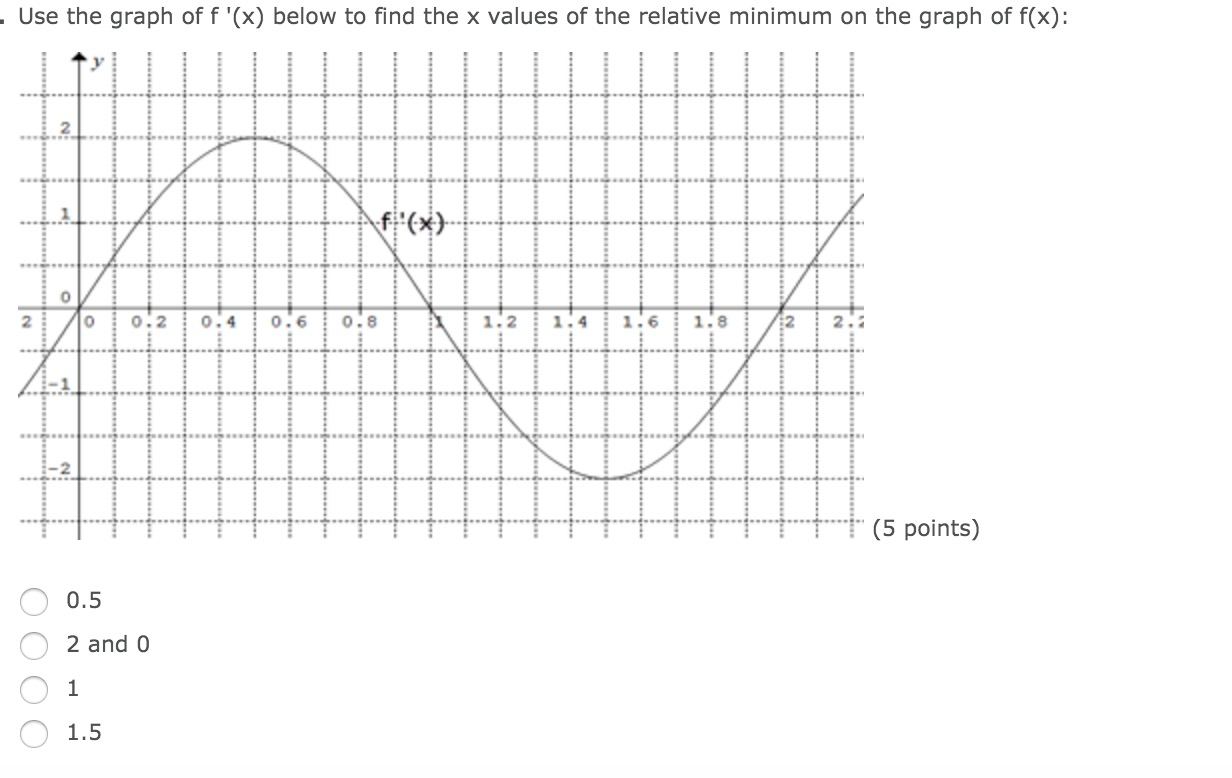



Use The Graph Of F X Below To Find The X Values Of Chegg Com



Transforming Graphs Of Functions Ppt Download
5 Sketch the graph of a function f(x) that satisfies the stated conditions Mark any inflection points by writing IP on your graph (Note there is more than one possible answer) a f is continuous and differential everywhere b f(0) = 3 c f'(x) > 0 on (60,4) and (0,00) d f'(x) < 0 on (4,0) e f"(x) < 0 on (0,2) f f"(x) > 0 on (2Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with − 1 1 in the expression f ( − 1) = − 8 ( − 1) 2 f ( 1) = 8 ( 1) 2 Simplify the result · Graph and Formula of f(x) g(x) New Resources Pythagoras' Theorem Area dissection 2;




Modulus Functions Sketching Graphs Edexcel A Level Maths Pure Revision Notes
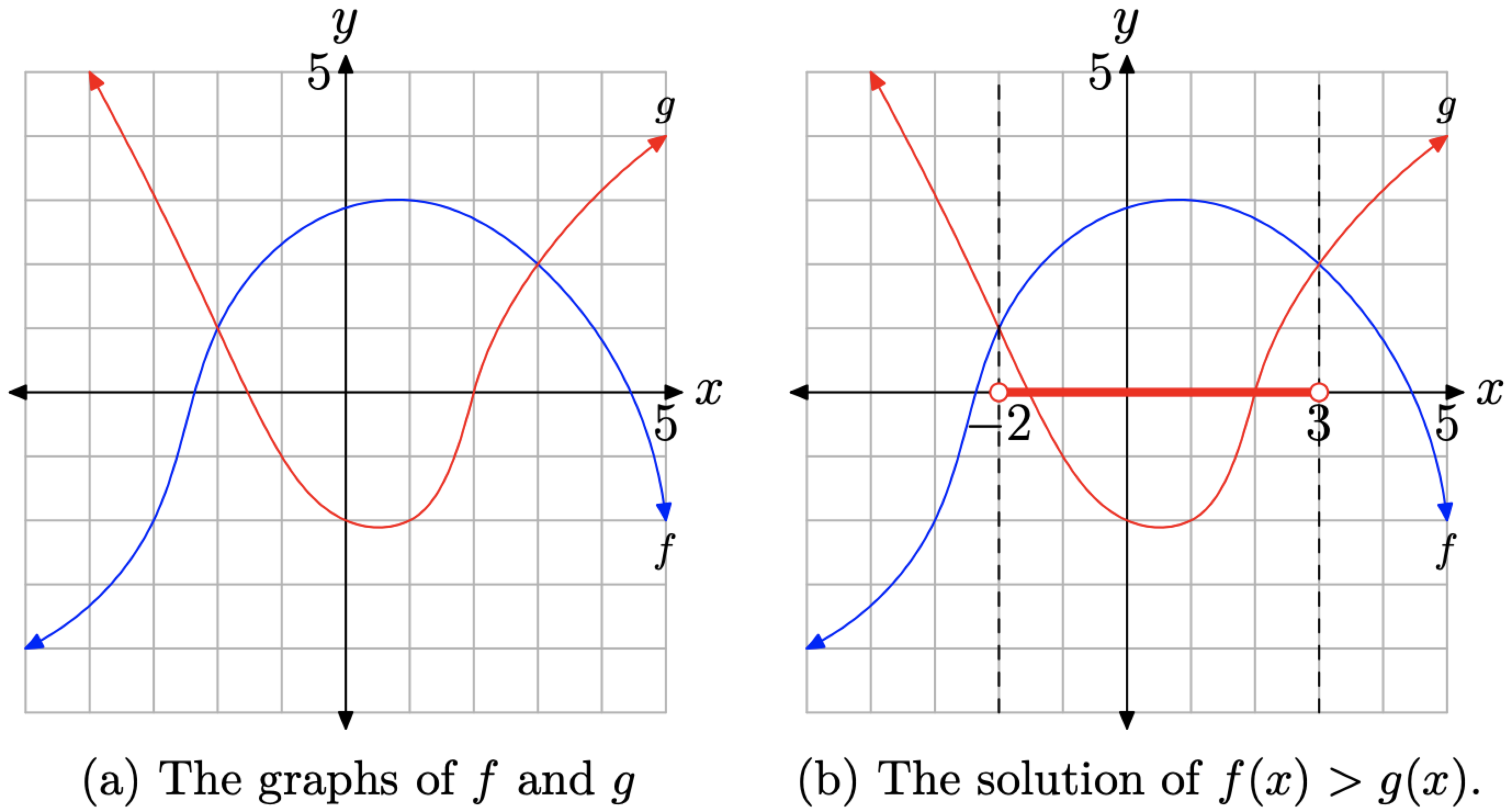



2 4 Solving Equations And Inequalities By Graphing Mathematics Libretexts
Answer to The graph of the function f (x) is shown Math; · The graph of f(x)=x^2 is called a "Parabola" It looks like this One of the ways to graph this is to use plug in a few xvalues and get an idea of the shape Since the x values keep getting squared, there is an exponential increase on either side of the yaxis You can see this by plugging in a few values When x=0, f(x)=0 x=1, f(x)=1^2=1 x=2,f(x)=2^2=4 x=3, f(x)=3^2=9 x=4, f(x · Correct answers 2 🔴 question How does the graph of g(x) = 3x 2 compare to the graph of f(x) = 3X?




Find The X Value At Which F Is Discontinuous Graph Mathematics Stack Exchange
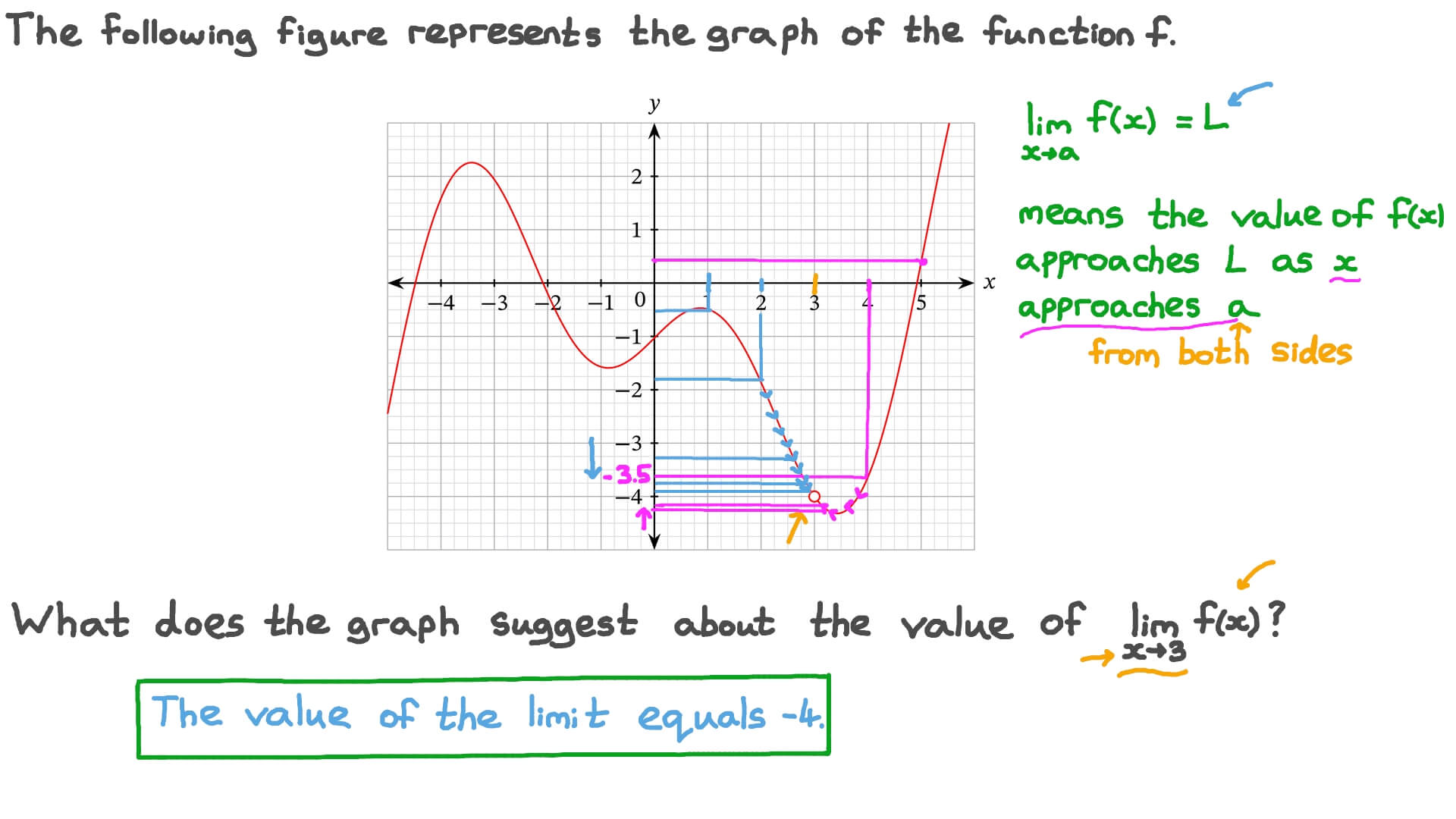



Question Video Finding The Value Of A Limit From A Graph Nagwa
Since the input \(x\) can be any real number the range of \(f\) is all the integers, \(\mathbb{Z}\) The function \(g(x)=xx\) which means it subtracts the whole number part, leaving only the fractional part of the input value \(x\) For integer values of \(x\), \(x=x\) which means that \(g(x)=0\) So the graph of the function looks like thisThe graph of f, shifted 3 units to the leftGraph of f ()x f ()xyy== Decreasing Increasing Horizontal tangent line ('flat' spot) possible max or min, but could be terrace point Vertical tangent line Cusp ''() dy fx y dx == Negative ≤ 0 Positive ≥ 0 = 0 DNE, (but f (x) exists) Determine from other info DNE, (but f (x) exists) Determine from other info () 2 2 "" dy fx y dx == DNE DNE Graph of f ()x




Exercise Chapter 3 Mathcfs Students Page
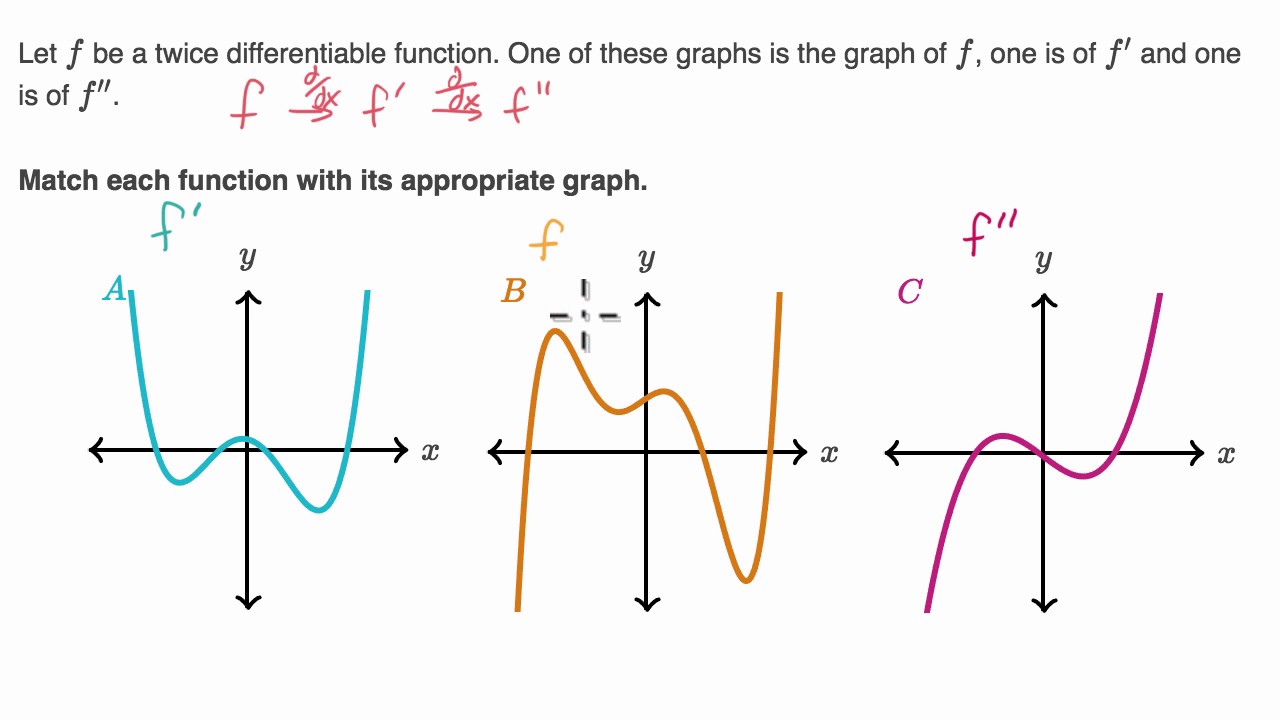



Identifying F F And F Based On Graphs Youtube
The simplest case, apart from the trivial case of a constant function, is when y is a linear function of x, meaning that the graph of y is a line In this case, y = f(x) = mx b, for real numbers m and b, and the slope m is given by = =, where the symbol Δ is an abbreviation for "change in", and the combinations and refer to corresponding changes, ieGraph The graph of the quadratic function p(x) = 7x2 is sketched with help of ordered pairs Construct a table of values with values of independent and dependent variable For some values of x evaluate the corresponding values of the function x − 2 − 1 0 1 2 p(x) 28 7 0 7 28 Plot the ordered pairs on a coordinate plane and join theImage Transcriptionclose Analyze the graph of the function f(x) = 3x 9 11 compared to the graph of the absolute value function g (æ) = x To obtain the graph of ƒ (x) = 3x 9 11, the graph of g (x) = æ has been • Shifted Click for List • Shifted Click for List by Number units by Number units • Vertically stretched by a factor of Number Which of the following best
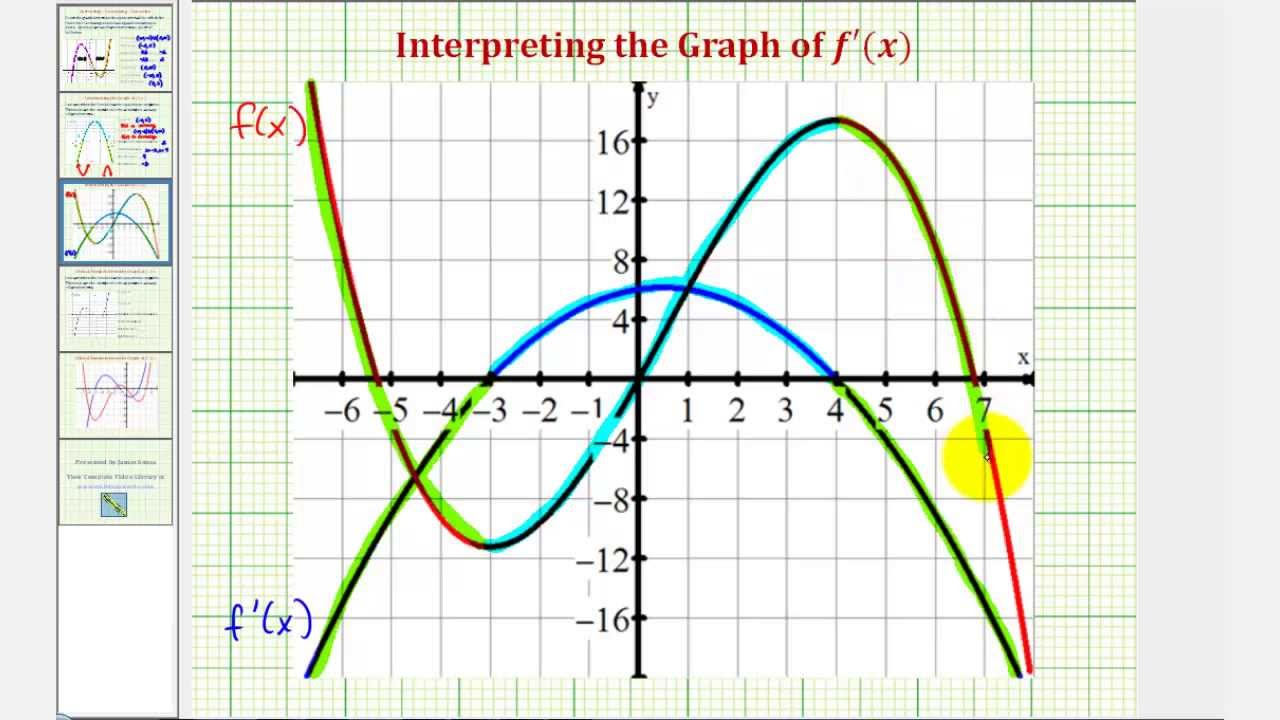



Ex 1 Interpret The Graph Of The First Derivative Function Degree 2 Youtube
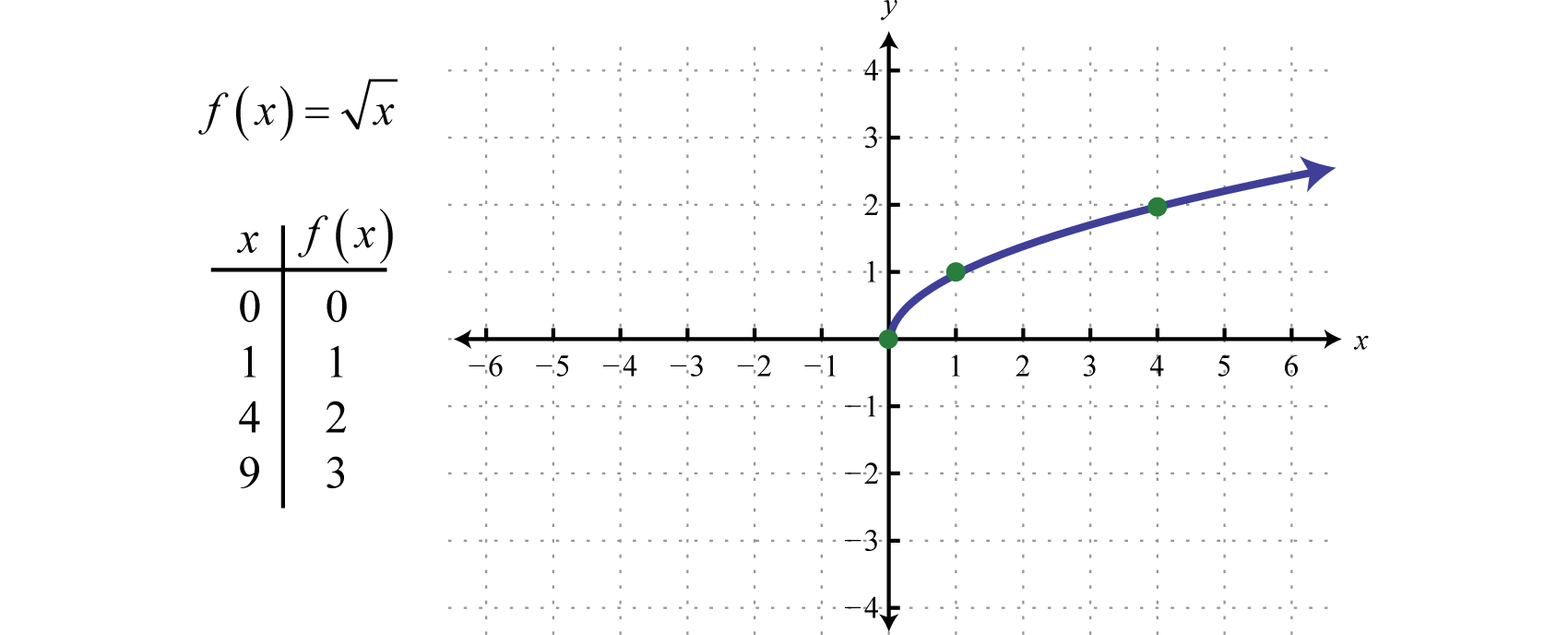



Graphing The Basic Functions
· The basic shape will remain the same Multiplying a function by a negative constant, − f(x), reflects its graph in the x axis Multiplying the values in the domain by − 1 before applying the function, f( − x), reflects the graph about the y axis WhenQuestion If (2, 8) is on the graph of y = f(x), then what point must be on the graph of y S (x)?Purplemath The last two easy transformations involve flipping functions upside down (flipping them around the xaxis), and mirroring them in the yaxis The first, flipping upside down, is found by taking the negative of the original function;




Quadratic Function Wikipedia




Visually Determining Antiderivative Video Khan Academy
Worked example matching a function, its first derivative and its second derivative to the appropriate graphSee the answer See the answer See the answer done loading Show transcribed image text Expert Answer Who are the experts?The graph of g(x) is a translation of f(x) 2 units left The graph of g(x) is a translation of f(x) 2 units right
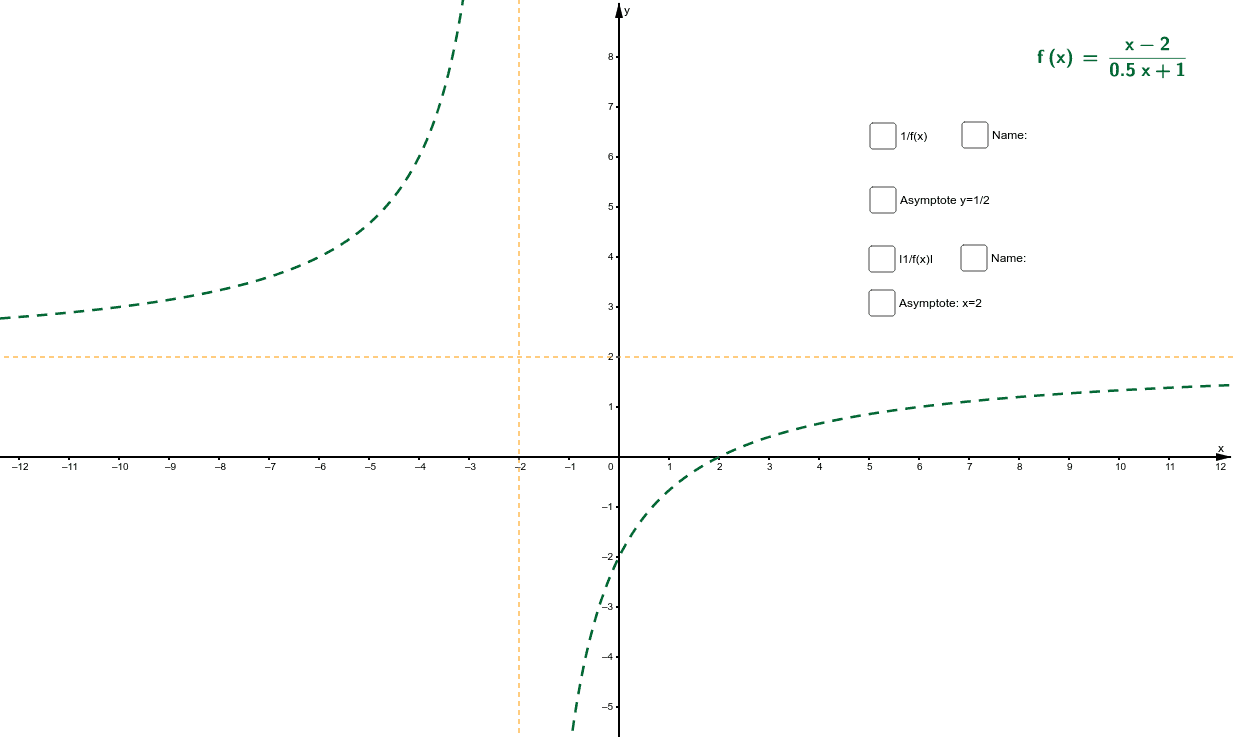



Drawing Graphs Of Y 1 F X And Y I1 F X I From Y F X Geogebra
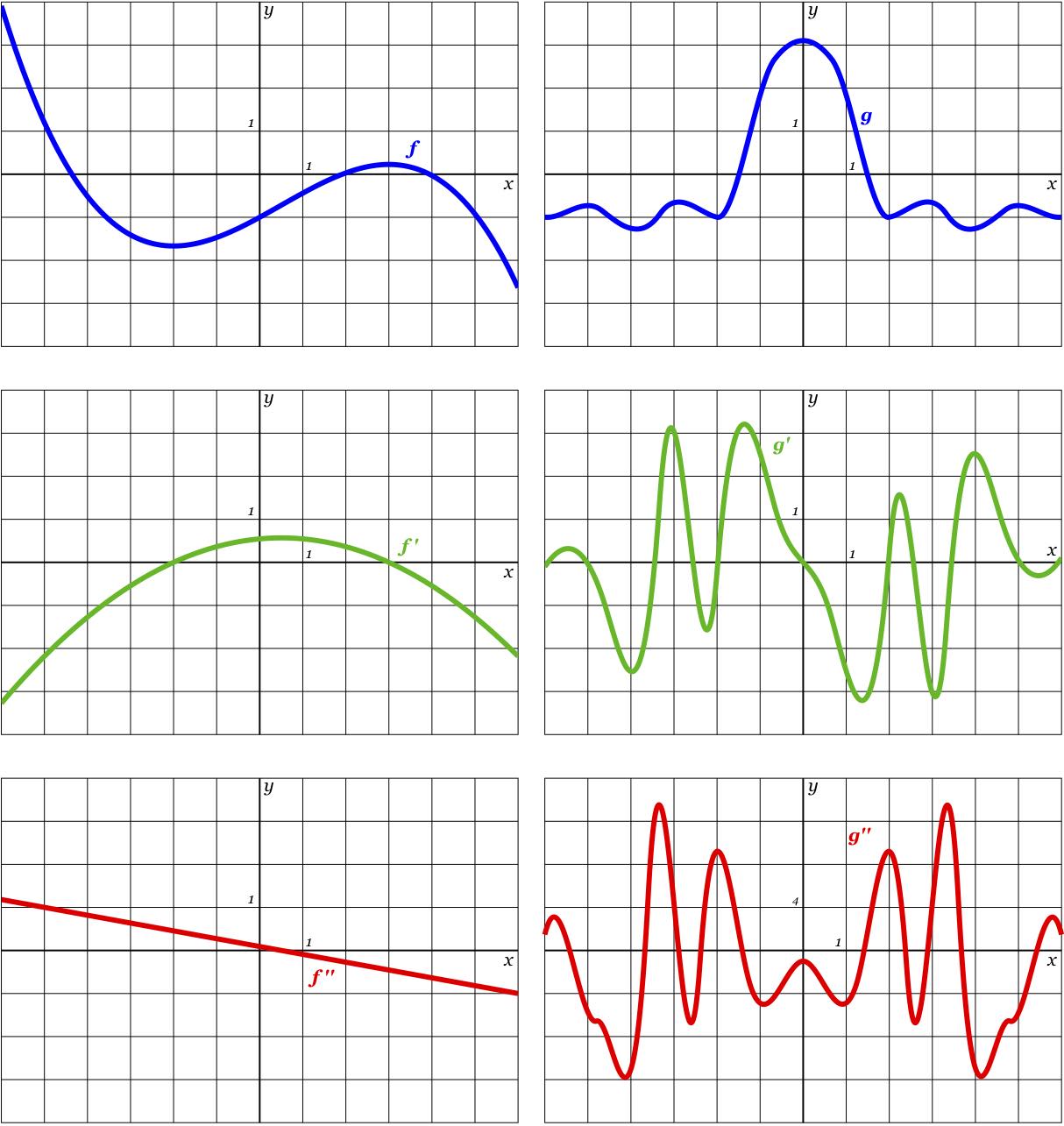



Cc The Second Derivative
14 The graph of f ( − x) is the mirror image of the graph of f ( x) with respect to the vertical axis The graph of − f ( x) is the mirror image of the graph of f ( x) with respect to the horizontal axis A function is called even if f ( x) = f ( − x) for all x (For example, cos ( x) )Hi, Can anyone help me understand the difference between the graphs of y= f(x) and y=f(x), please?In this video I show you the graphical relationship that exists between y = f(x) and its inverse function y = f 1(x) Example (1) Example in the video If f(x) = x2 1, x ε ℝ, x ≥ 0 Find the range of f(x) Find f 1(x) and state
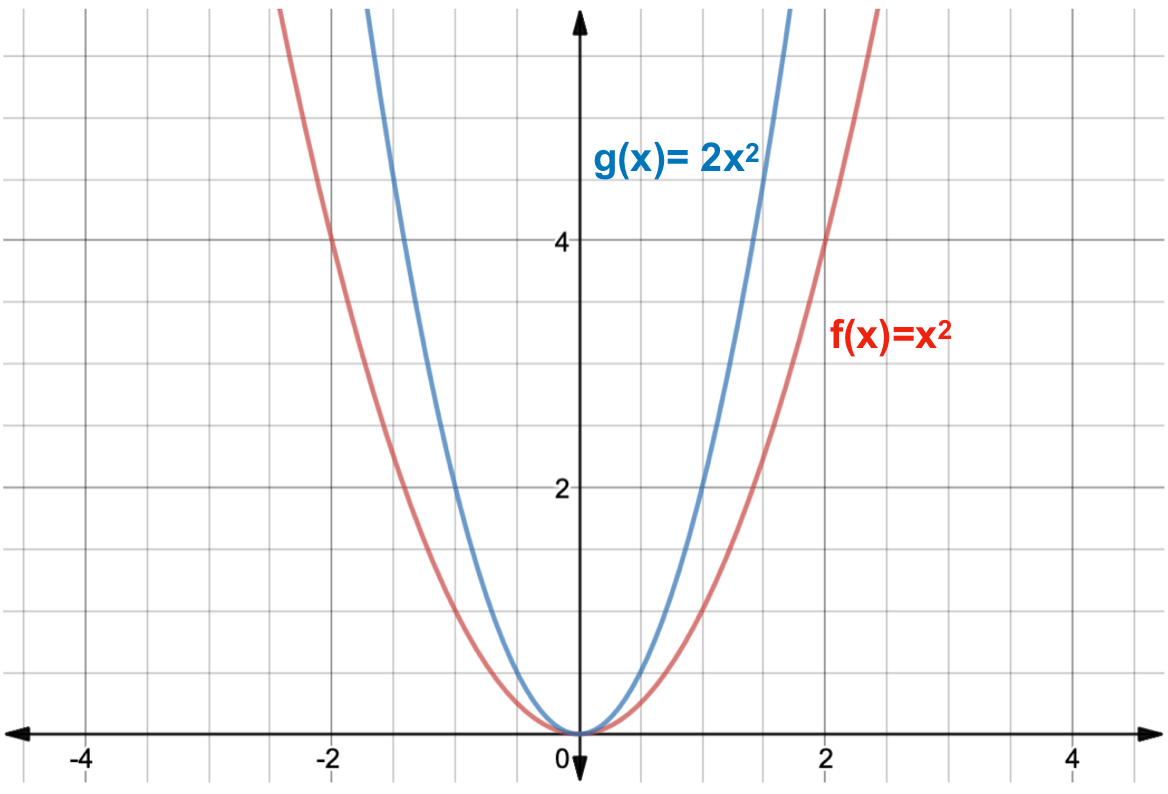



What Is A Function Transformation Expii
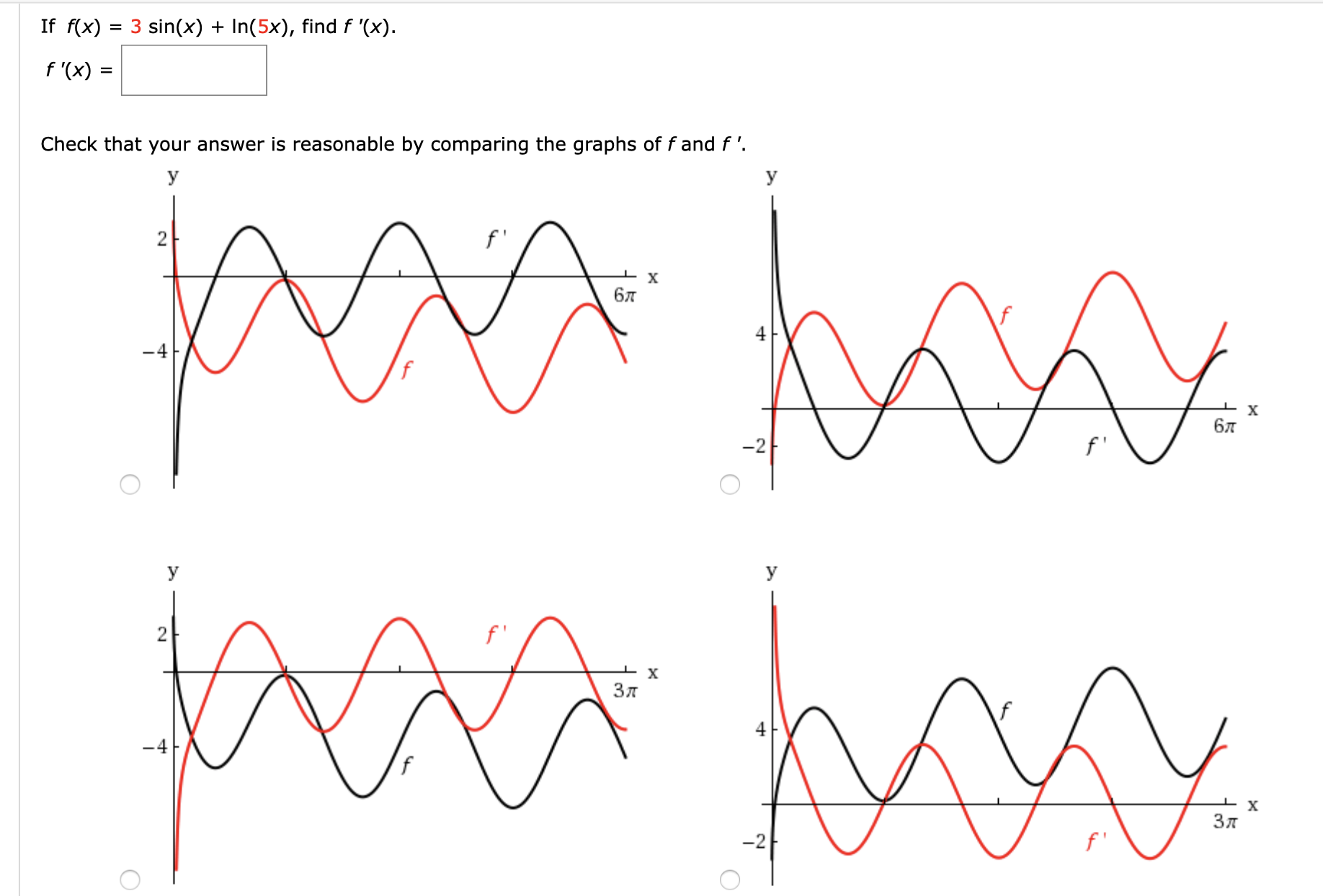



Answered 3 Sin X In 5x Find F X If F X Bartleby
Calculus questions and answers; · The image below shows the graph of f(x) Graph g(x) using the fact that it is the result of f(x) being stretched horizontally by a factor of 1/2 Make sure to include the new critical points for g(x)I understand that for y=f(x) you just reflect the parts of the graph below the x axis in the x axis as with any modulus graph, but I don't understand how y=f(x) is different I feel like it should just be the same?




Graphing Translations G X F X C Or G X F X C Youtube
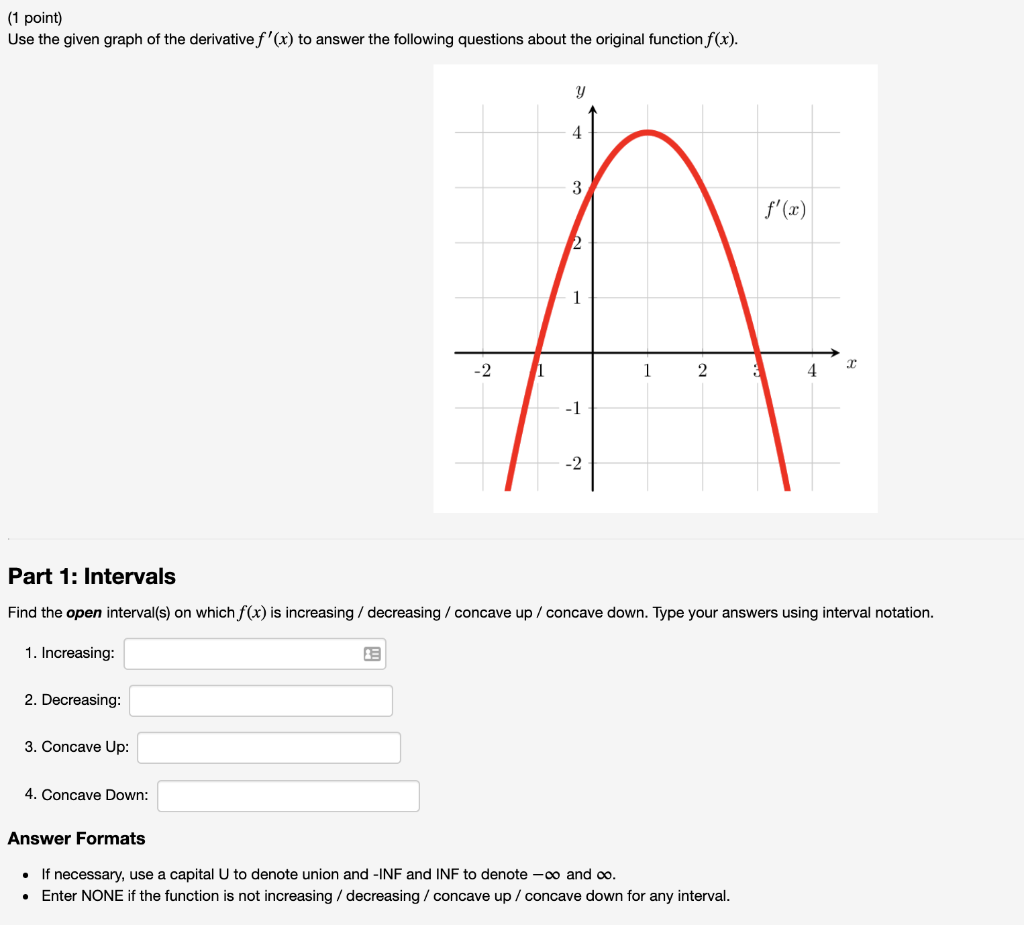



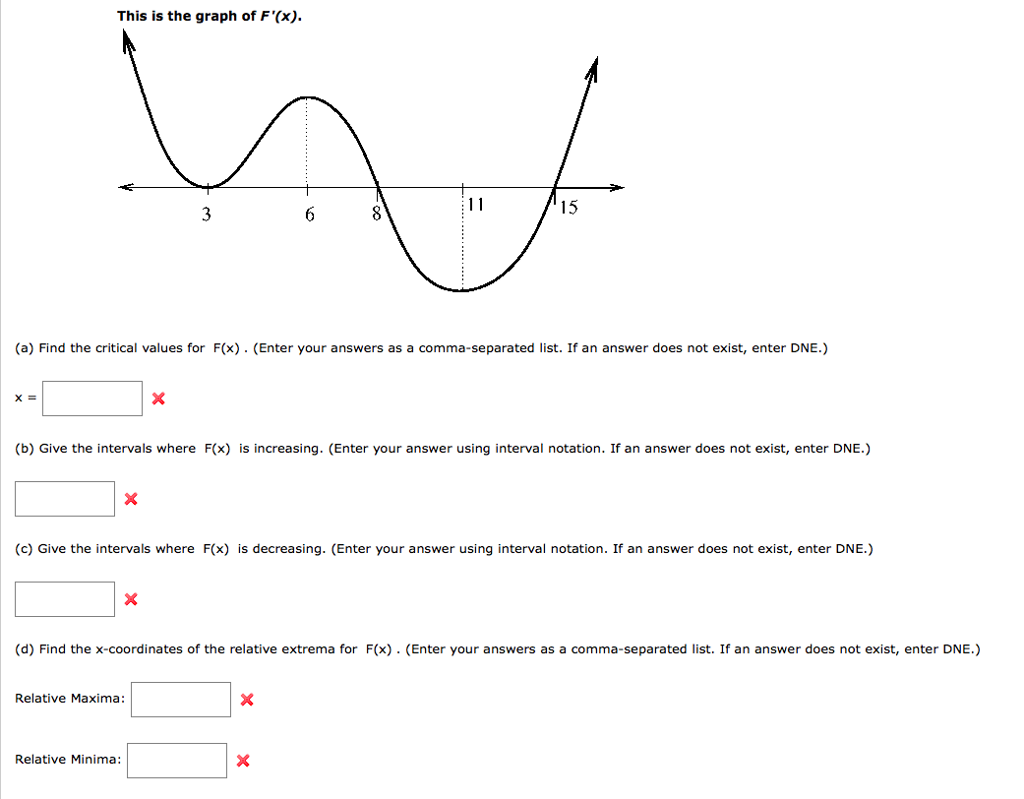
Solved 1 Point Use The Given Graph Of The Derivative F Chegg Com
The graph of g(x) is a translation of f(x) 2 units left O The graph of g(x) is a translation of f(x) 2 units right O The graph of g(x) is a translation of f(x) 2 units up O The graph of g(x) is a translation of f(x) 2 units downTranslation in the xdirection Translation in the ydirection Reflection in the ydirection 4 · For instance, if I have f(x)=(x) 3 3, then the graph would translate three units upwards Reflection Reflection is different compared to translation To investigate this transformation, consider the signs of the inputs and outputs y=f(x) will indicate that the graph has reflected about the xaxis




2 5 Vertical Transformations Mathematics Libretexts



Log Log Plot Wikipedia
Purplemath There are two other transformations, but they're harder to "see" with any degree of accuracy The first of these transformation is multiplication on the entire function To see what this looks like, compare the graphs of 2 × f (x) = 2x2, f (x) = x2, and ½ × f (x) = (½) x2, below graph of 2 × f (x) = 2x2 (This is skinnierIt's been stretched parallel to the yaxis by a factor of 2 and finally f (2x) Taking the graph of f (x) = x^2 again, this would give us the graph (2x)^2 = 4x^2, which is compressed horizontally by a factor of a half In summary f (x) a is f (x) shifted vertically a units f (x – a) is f (x) shifted horizontally a unitsGraph functions using reflections about the xaxis and the yaxis Another transformation that can be applied to a function is a reflection over the x – or y axis A vertical reflection reflects a graph vertically across the x axis, while a horizontal reflection reflects a graph horizontally across the y



Understanding F X Function And How To Graph A Simple Function Math Algebra Graphing Functions F If 7 F If 4 Showme
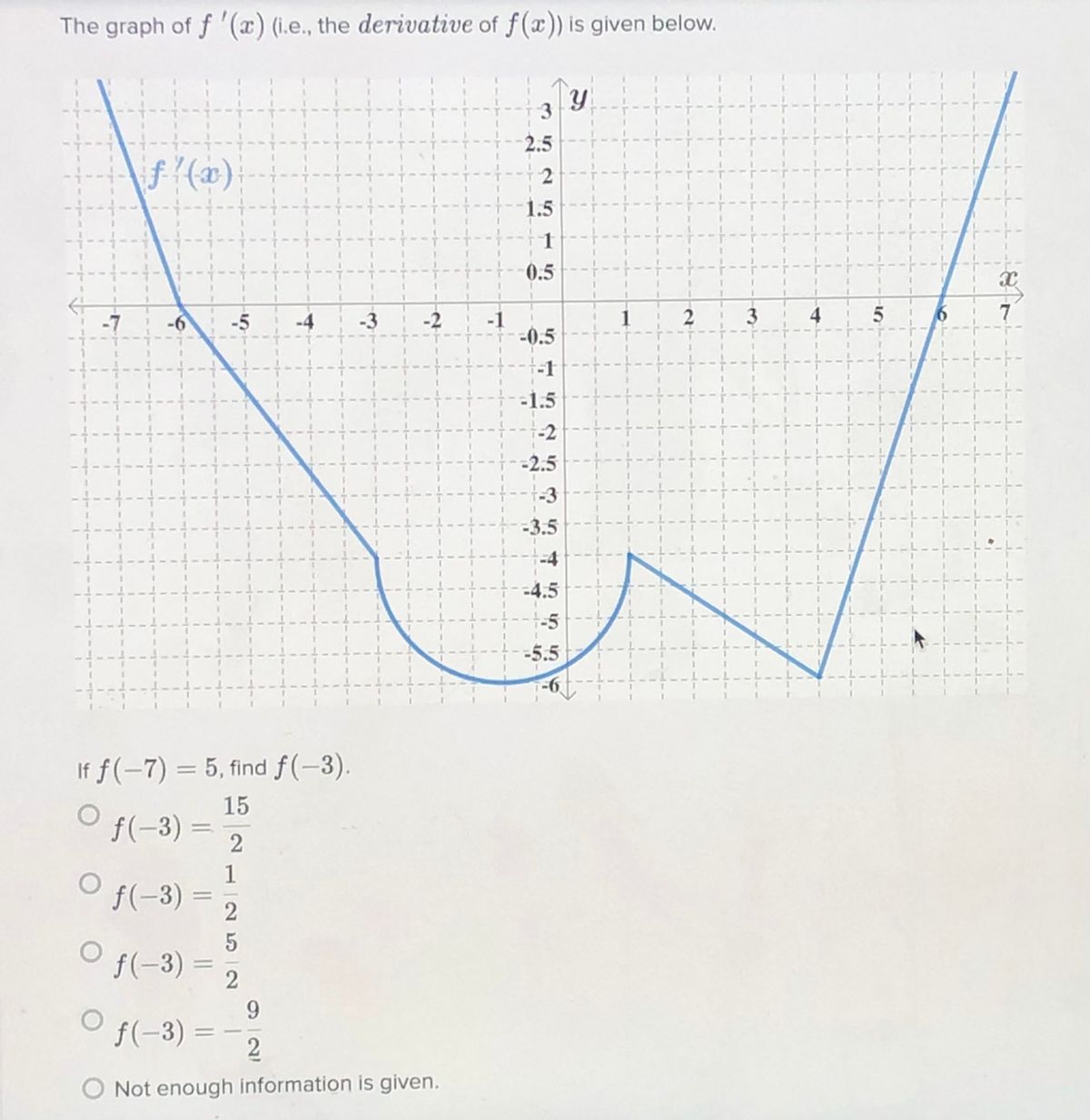



Answered The Graph Of F X I E The Bartleby
Yes they are The placement of the parentheses makes a difference For example with your graph above, when x = 4, f(x) = 0 and hence f(x) 2 =0 2 = 2 But f(x 2) = f(4 2) = f(2) = 2 In the second expression, since 4 2 is inside the parentheses you evaluate it first to get 2 and then use the table for y = f(x) to find f(2) Cheers,If y = f(x), the graph of y = af(x) is ), parallel to the xaxis Scale factor 1/a means that the "stretch" actually causes the graph to be squashed if a is a number greater than 1 Example · Compared to the graph of the function #f(x) = sqrtx#, how is the graph of #g(x)= sqrt(x8)4# translated?
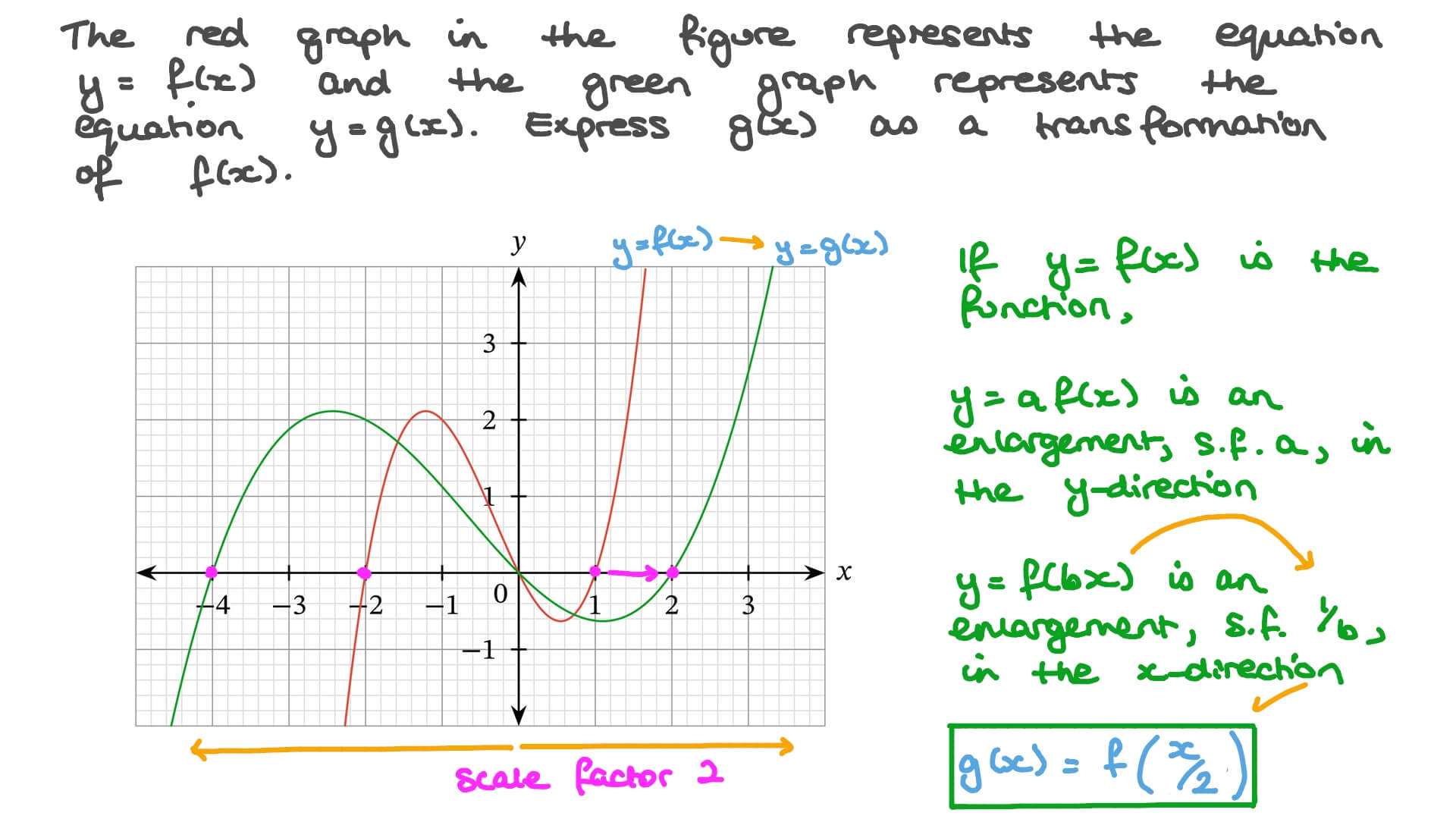



Question Video Transformations Of Graphs Nagwa
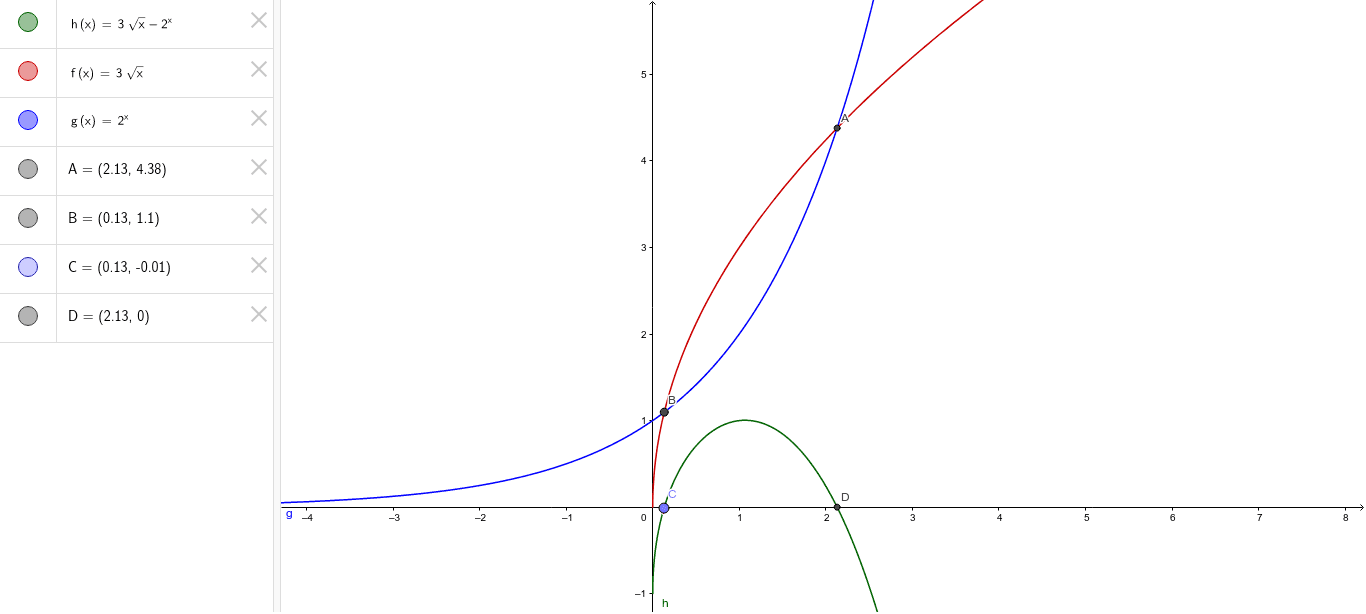



Graph Of F X G X F G X Geogebra
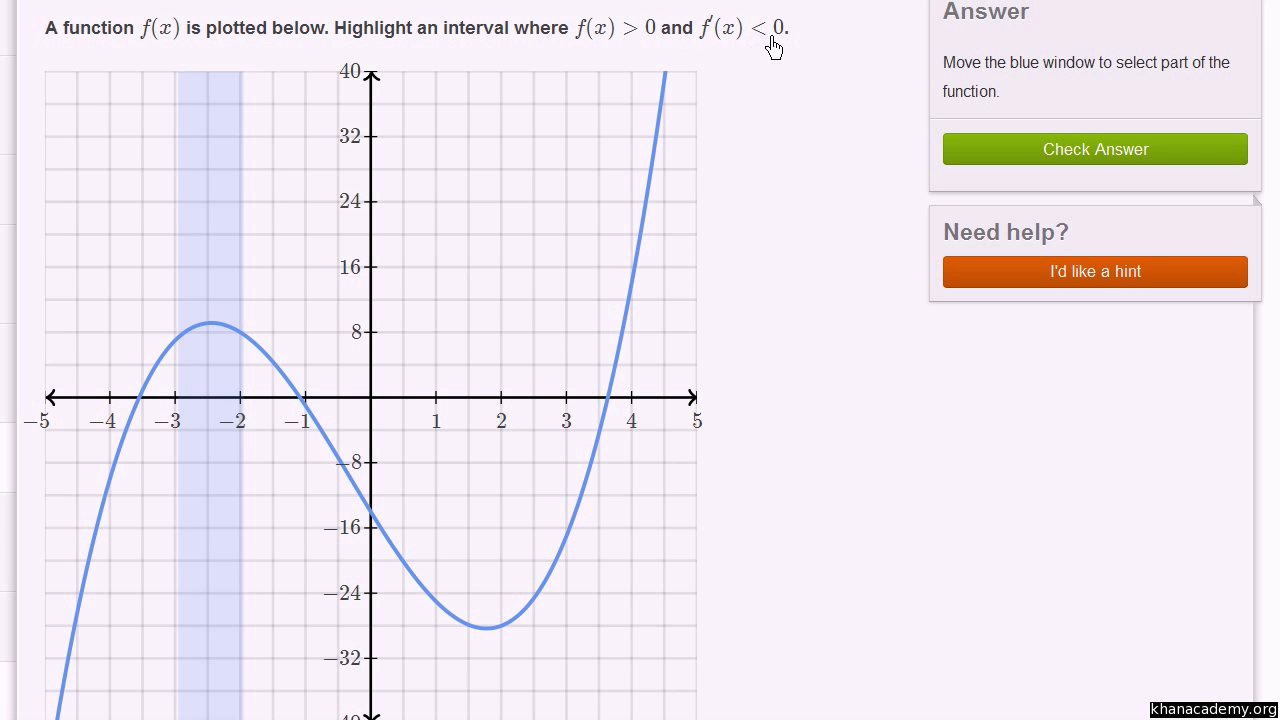



Derivative The Direction Of A Function Video Khan Academy
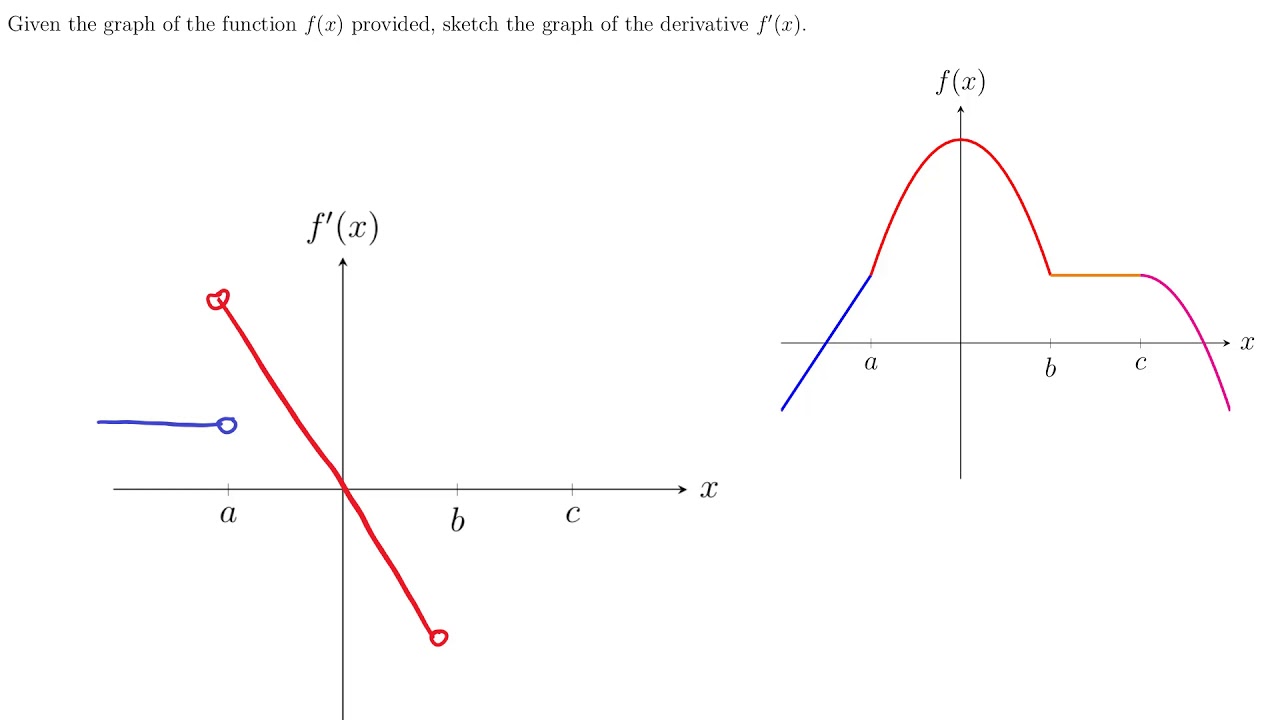



The Derivative Function
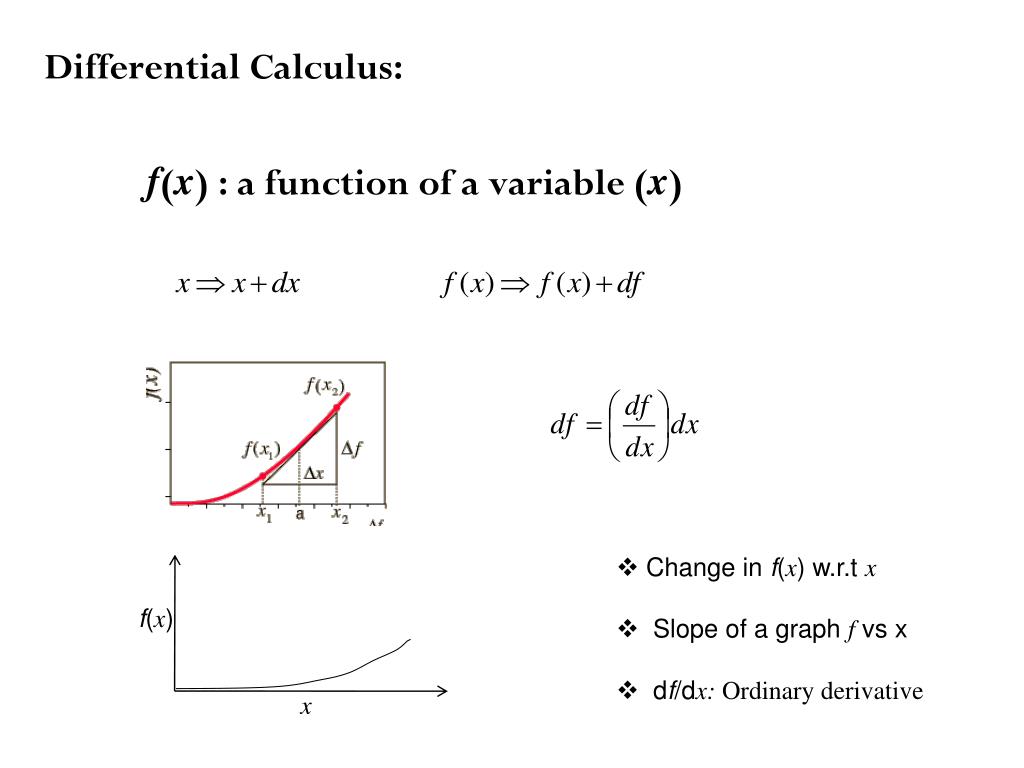



Ppt Differential Calculus F X A Function Of A Variable X Powerpoint Presentation Id
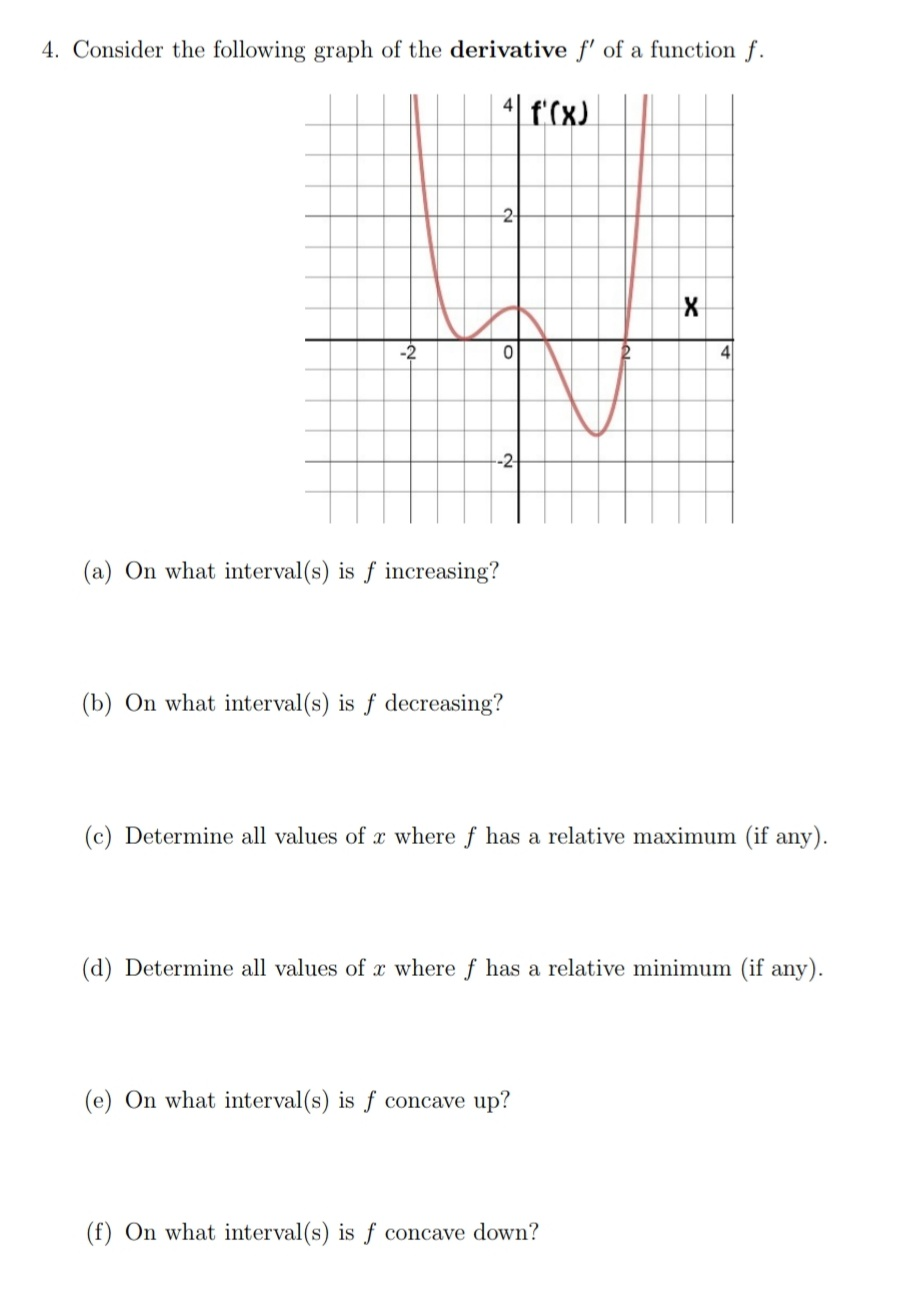



4 Consider The Following Graph Of The Derivative F Chegg Com




Finding Max Min Inflection Pts Given The Graph Of F X Or F X Youtube
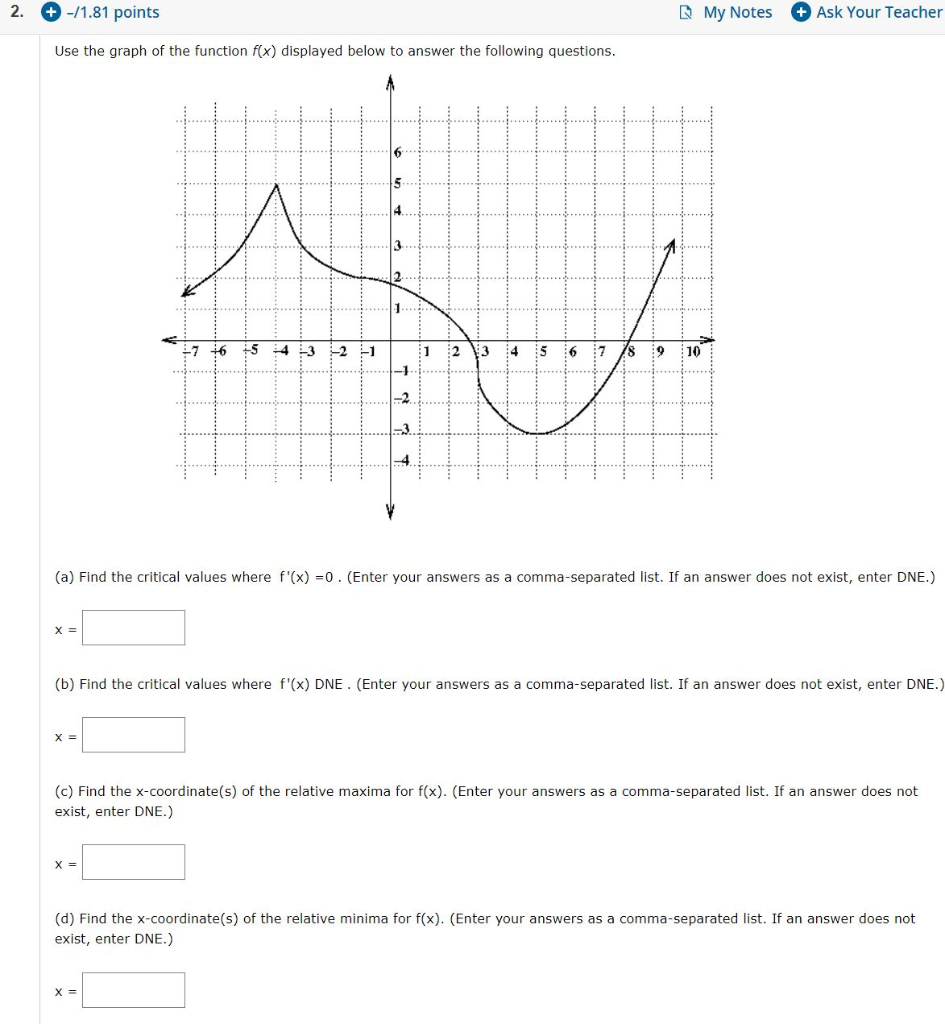



Solved 2 11 81 Points My Notes Ask Your Teacher Use Chegg Com
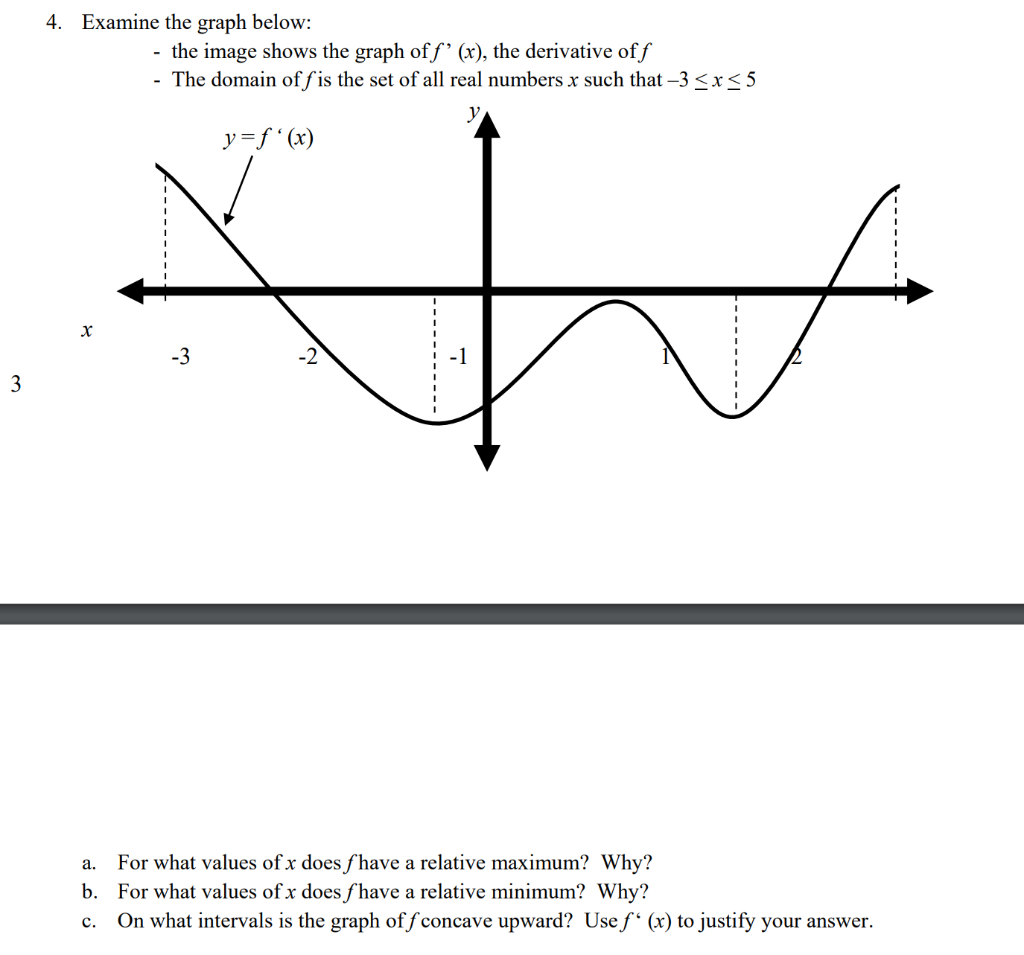



Solved 4 Examine The Graph Below The Image Shows The Chegg Com



Transforming Graphs Of Functions Ppt Download
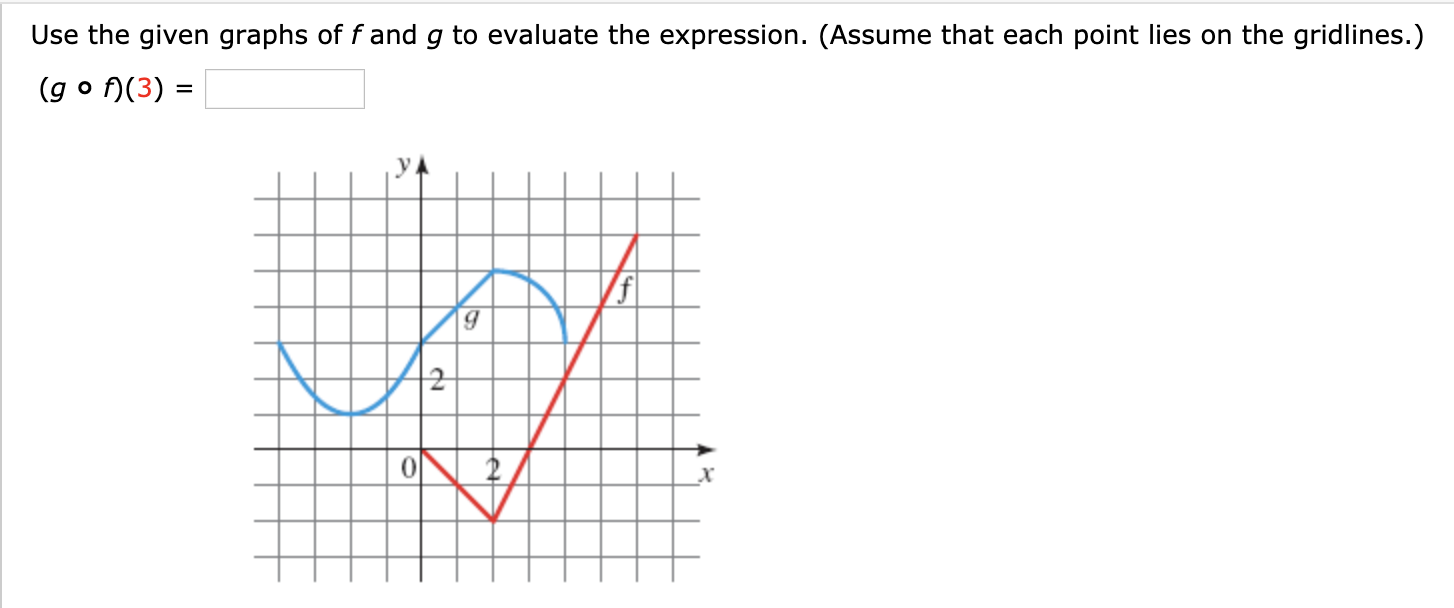



Answered Use The Given Graphs Of F And G To Bartleby



College Algebra Is The Product Of Real Linear Factors But If F X 0 Has Imaginary Or Complex Roots F X Containsquadratic Factors Of The Type X A 6 Which Cannot
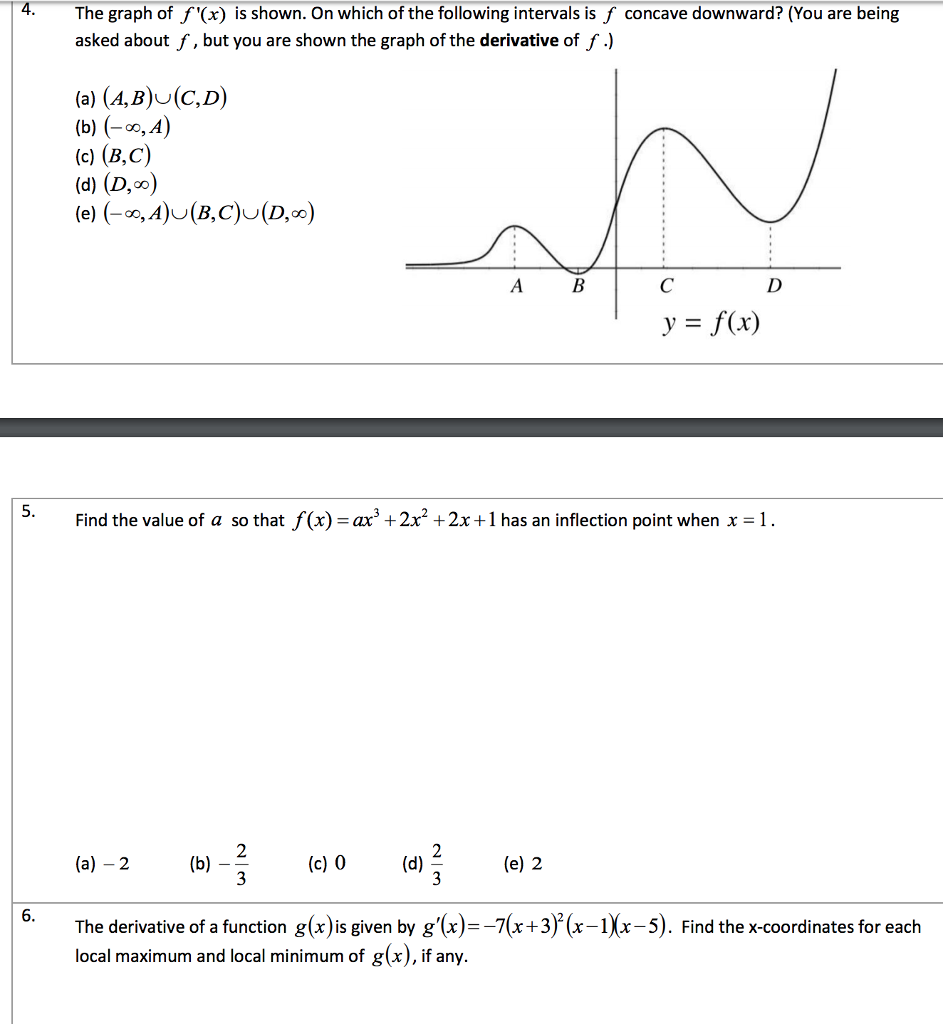



4 The Graph Of F X Is Shown On Which Of The Chegg Com
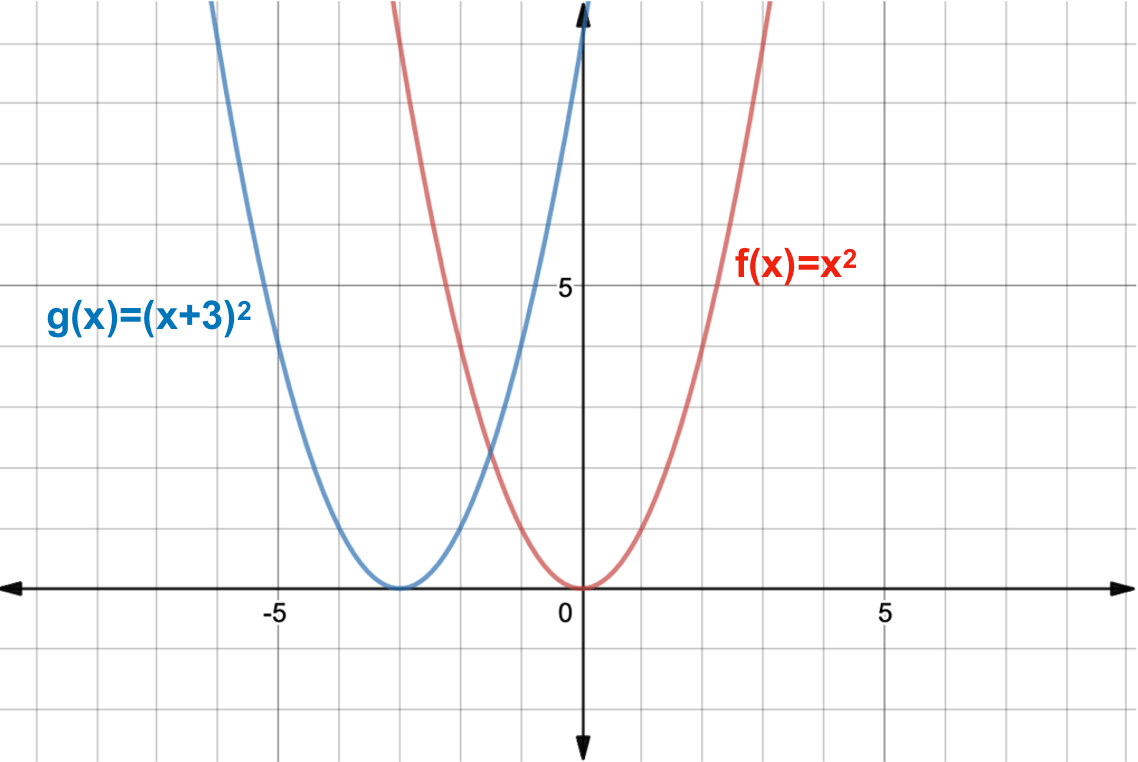



What Is A Function Transformation Expii



Draw The Graph Of F X Ln 1 Ln X Find The Point Of Inflect
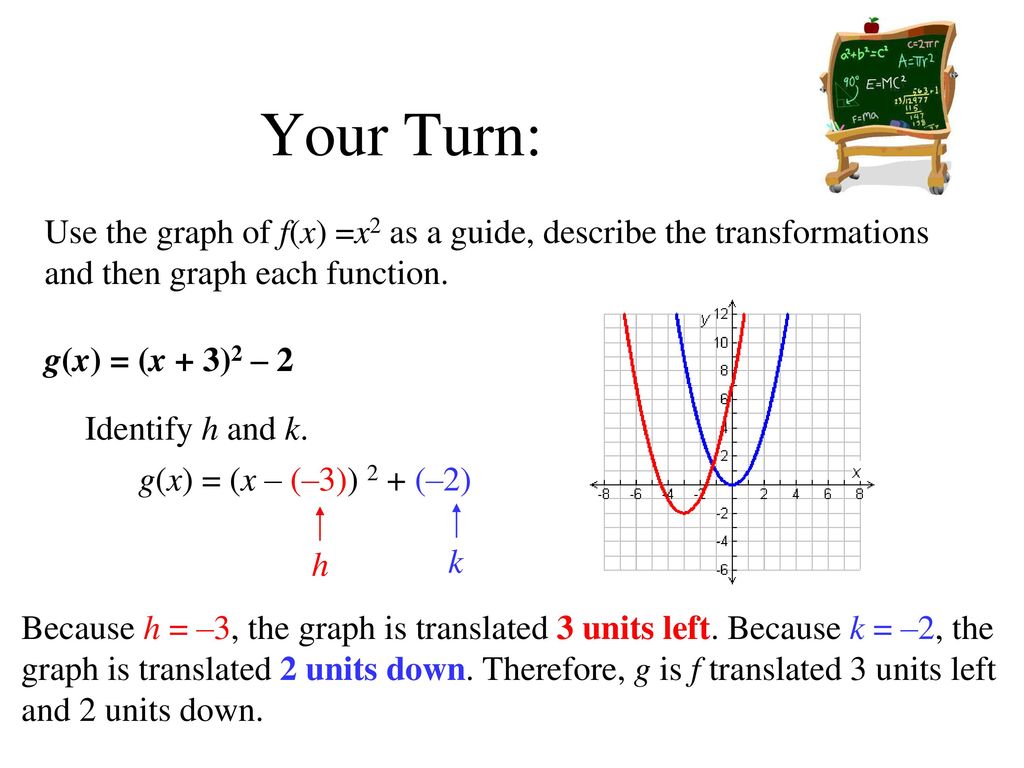



Quadratic Functions And Transformations Lesson Ppt Download



Functions Inverse And Composite Functions
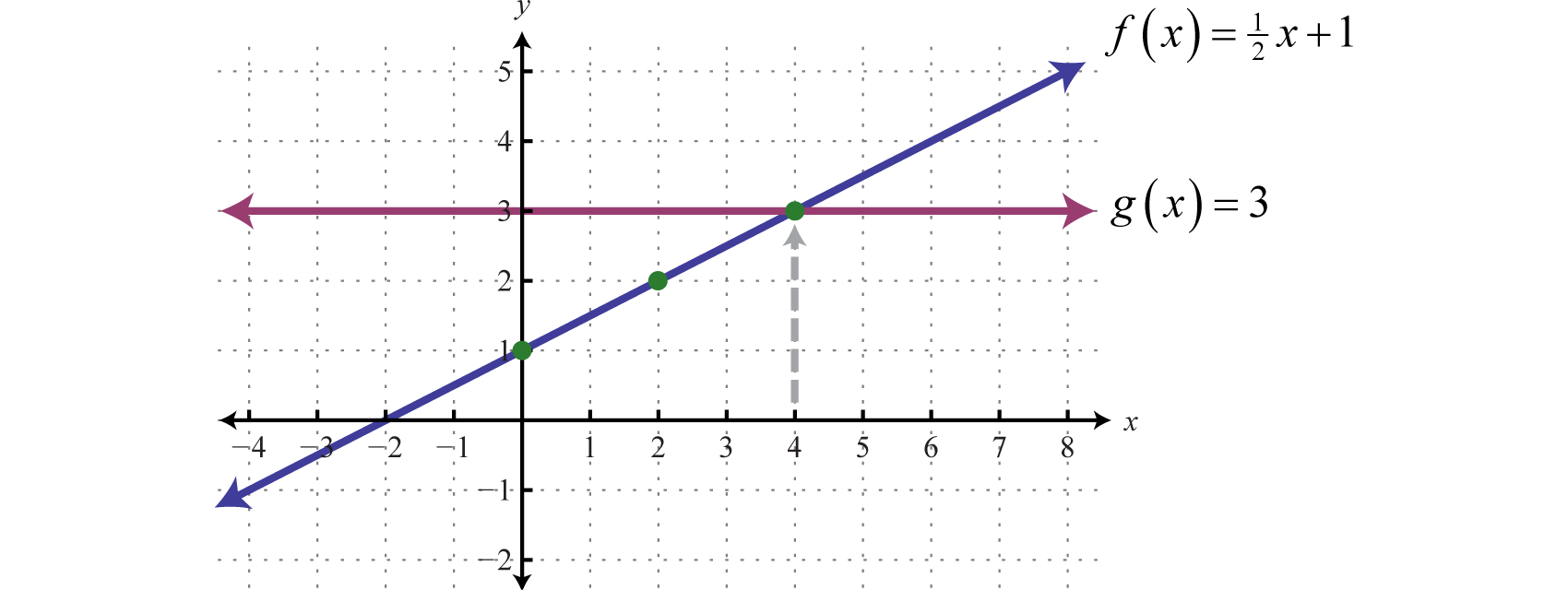



Linear Functions And Their Graphs
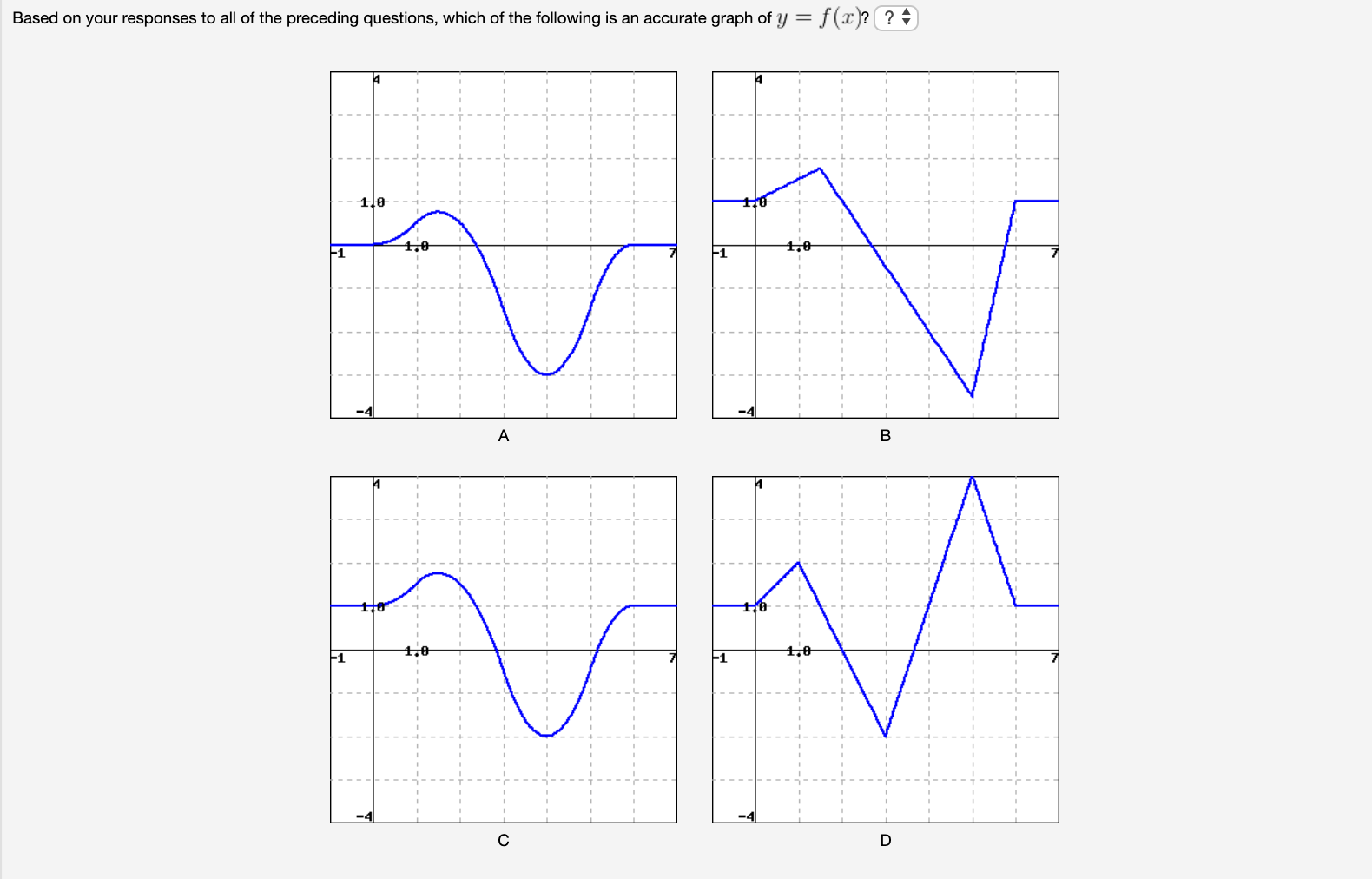



Answered Suppose That The Following Information Bartleby
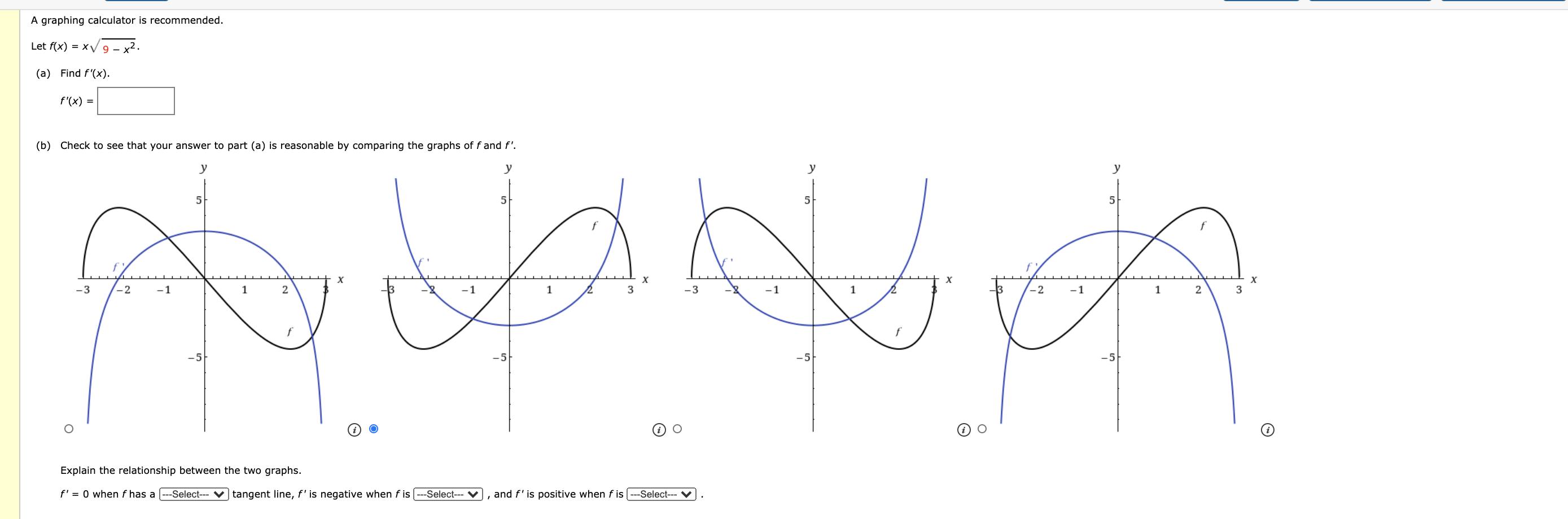



A Graphing Calculator Is Recommended Let F X Chegg Com



Graphing Shifted Functions Video Khan Academy




Shift Function Up Or Down F X C Expii
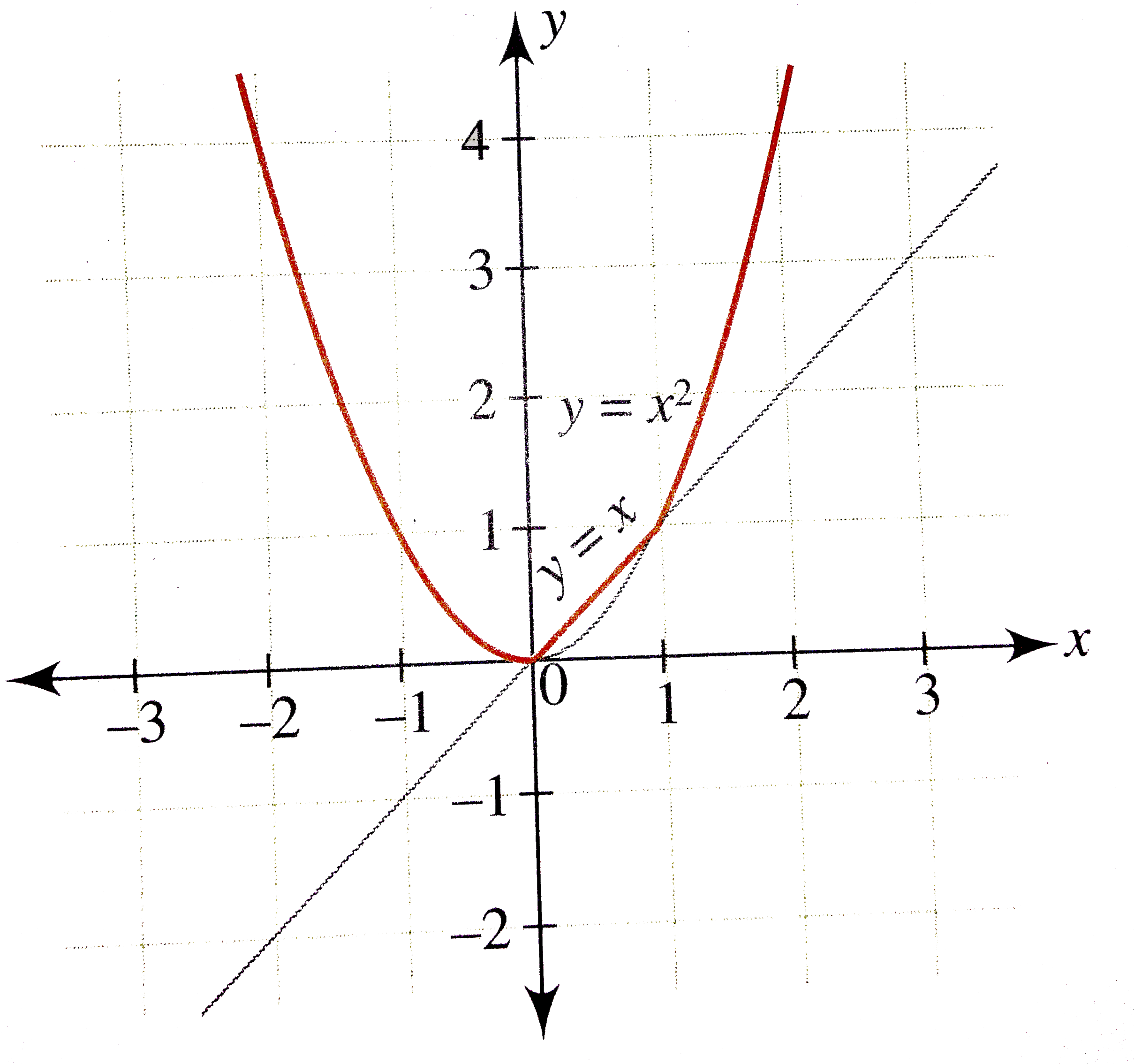



Draw The Graph Of The Function F X Max X X 2 And Write
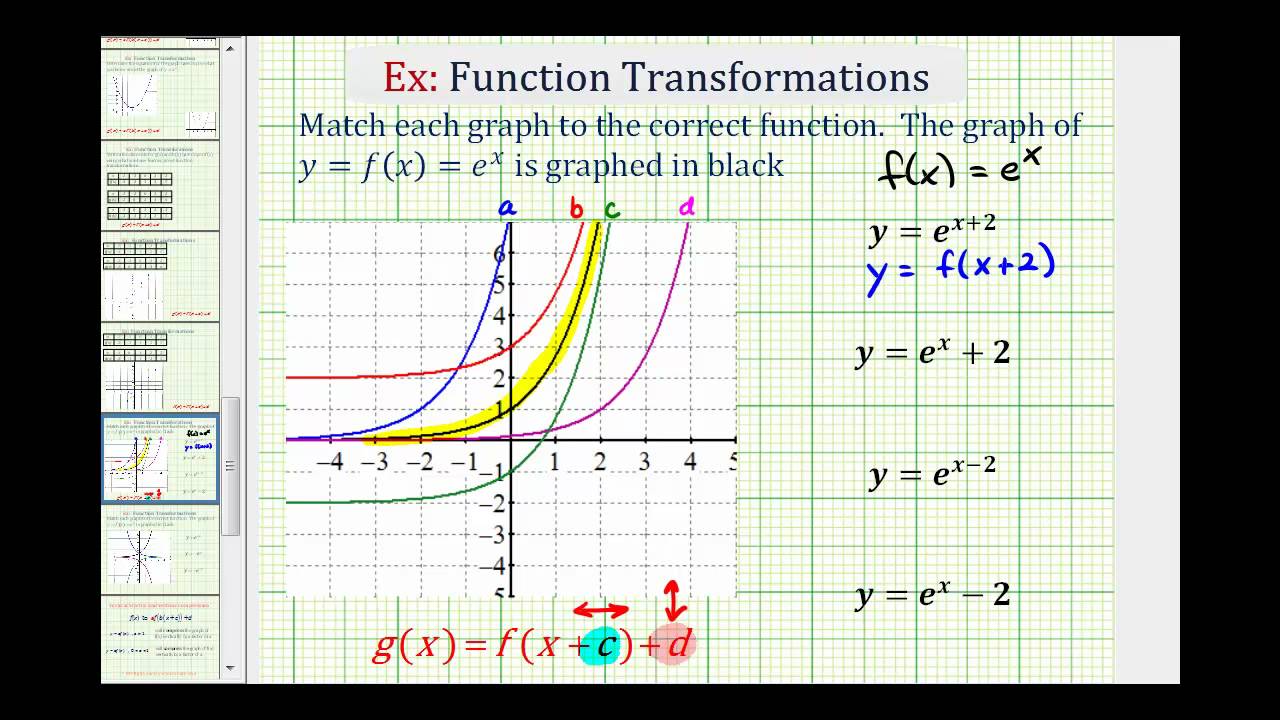



Horizontal And Vertical Translations Of Exponential Functions College Algebra
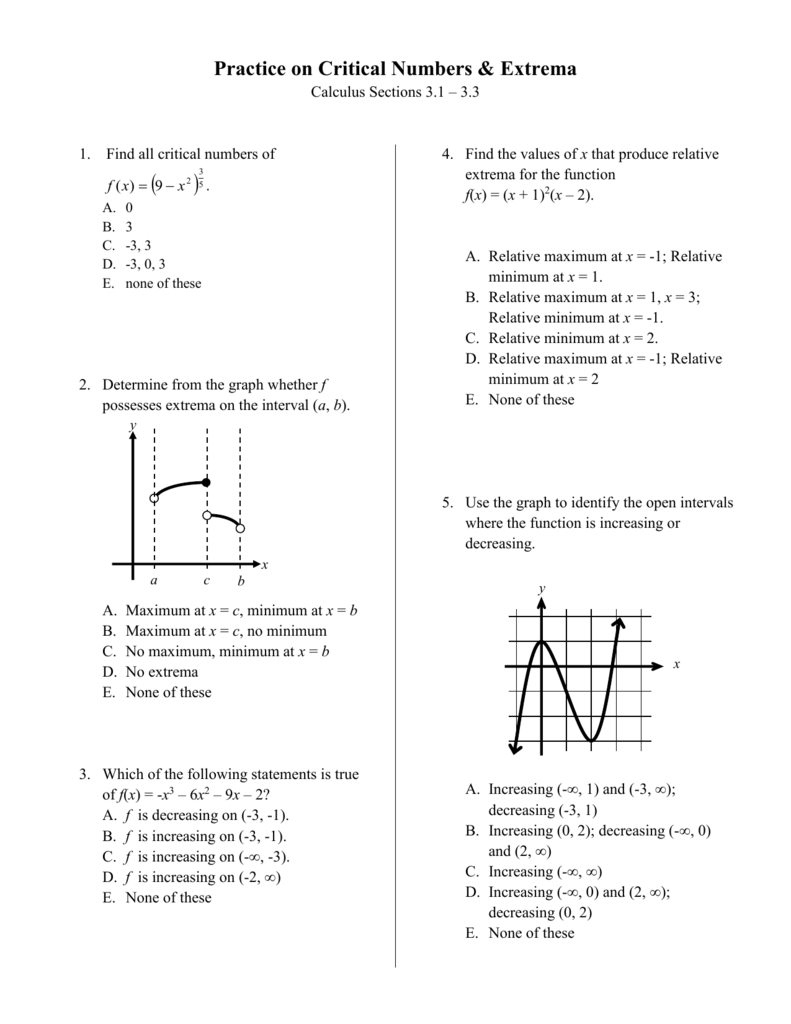



Practice On Critical Numbers Extrema




Worked Examples Finding Definite Integrals Using Algebraic Properties Video Khan Academy




Reflecting Functions Examples Video Khan Academy




Finding Values Of Derivative Given F Graph Mathematics Stack Exchange




Comparing Functions Quadratic Students Are Given The Graph Of F X X2 And Are Asked To Compare T
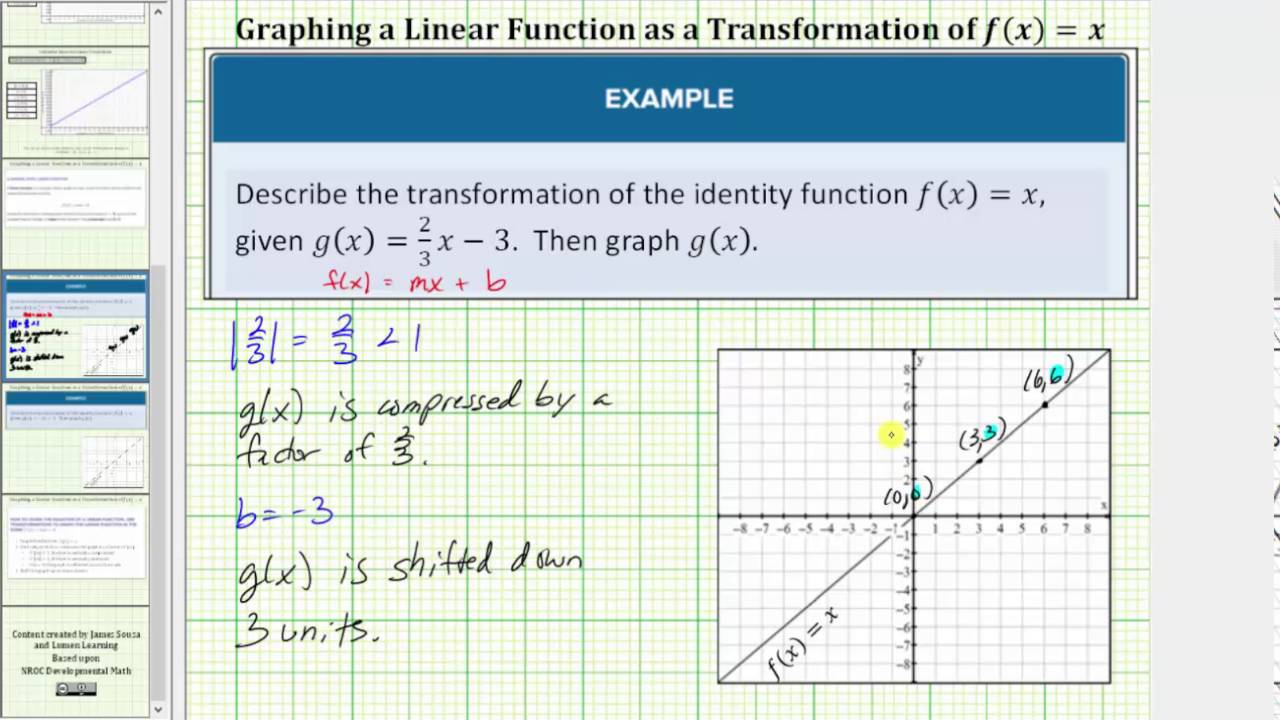



Graph A Linear Function As A Transformation Of F X X Youtube



Geogebra Tutorial Functions
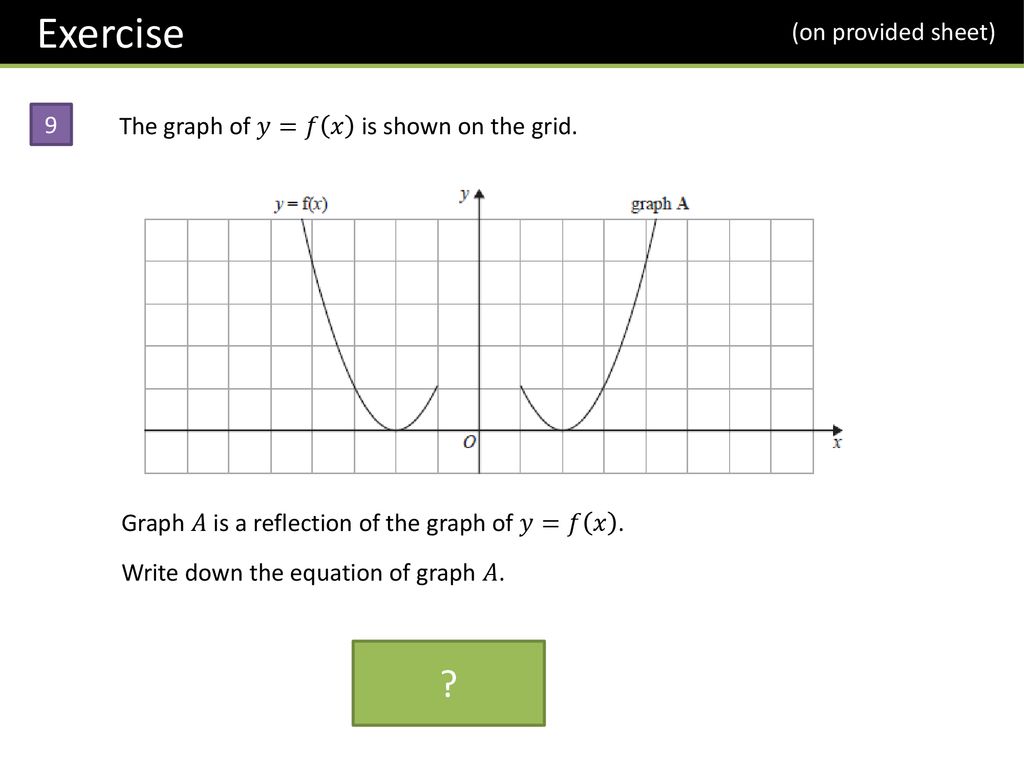



Gcse Graph Transformations Ppt Download




Finding The Derivative Of A Function Looking At A Graph Mathematics Stack Exchange
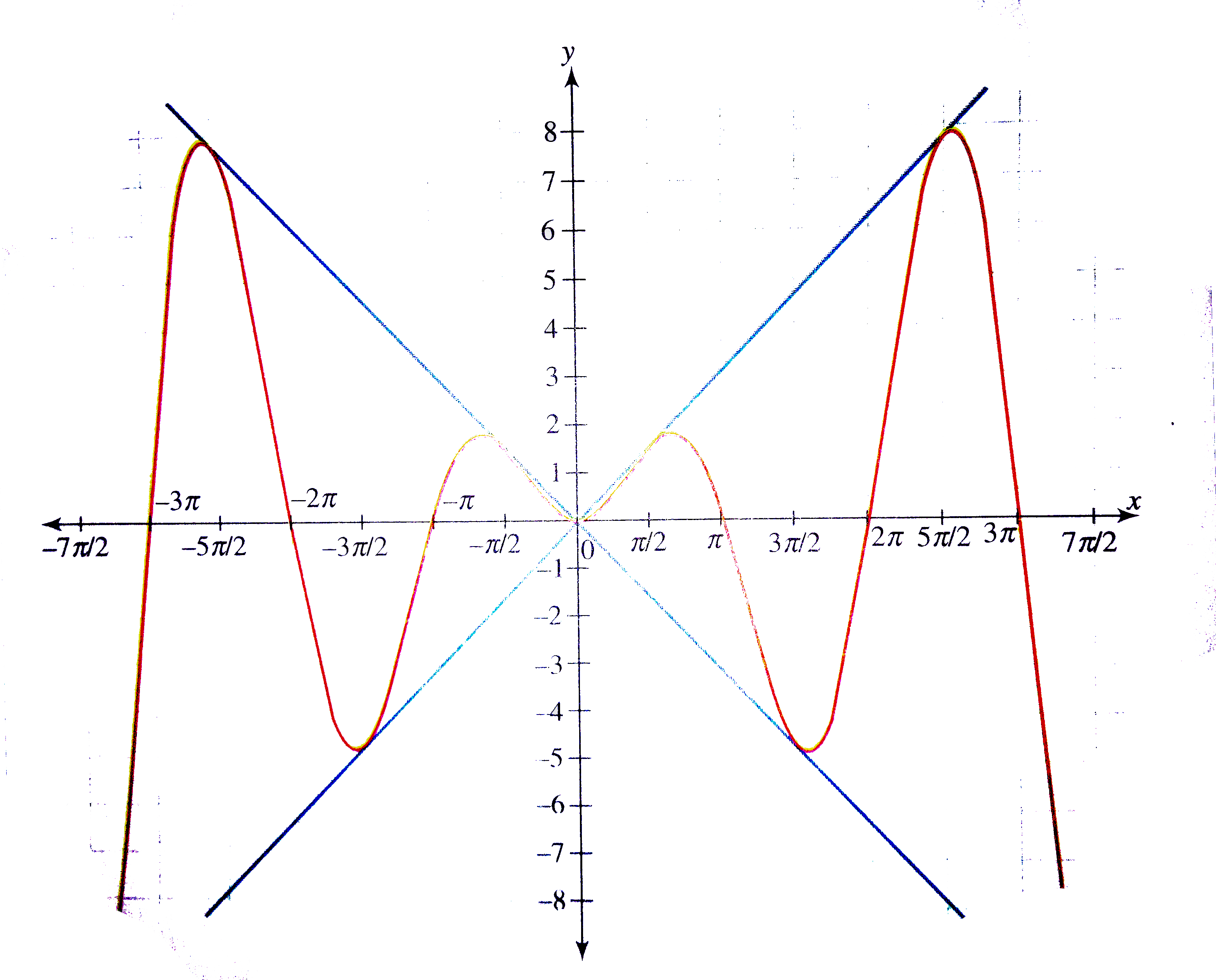



Draw The Graph Of Y X Sin X



Calculus Limit Function Take The Limit As X Approaches
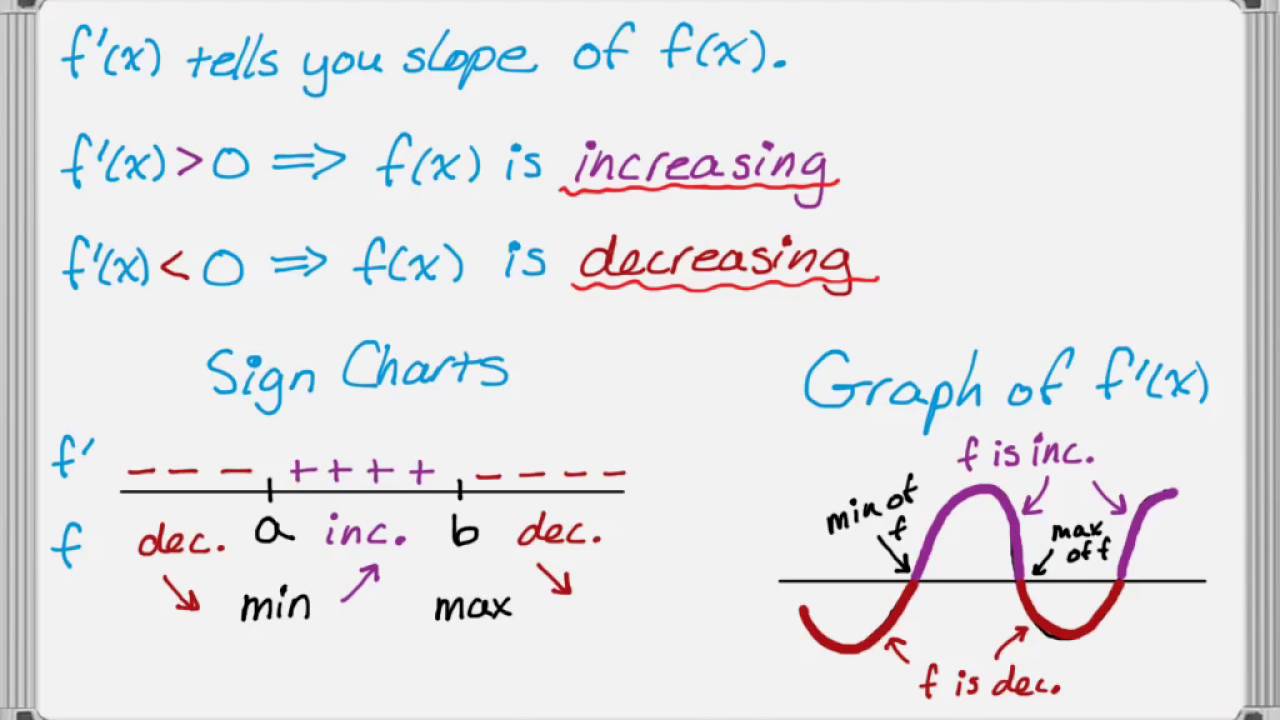



Using The First And Second Derivatives To Graph Function Youtube
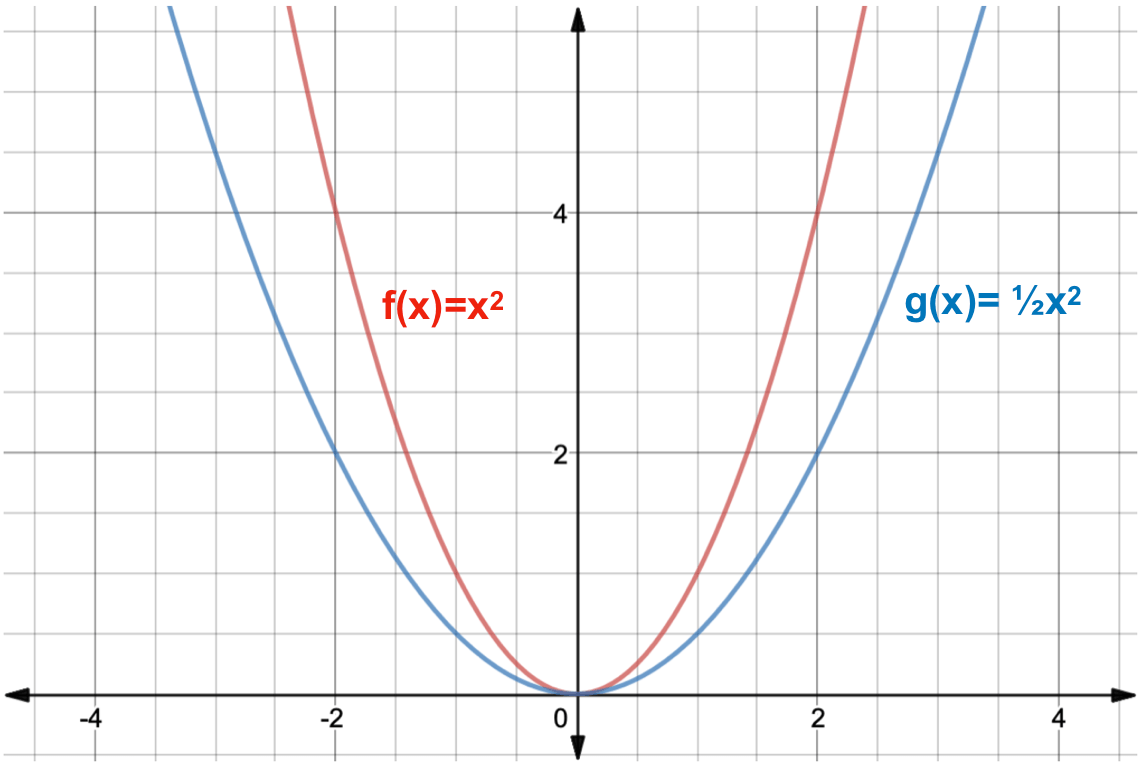



What Is A Function Transformation Expii
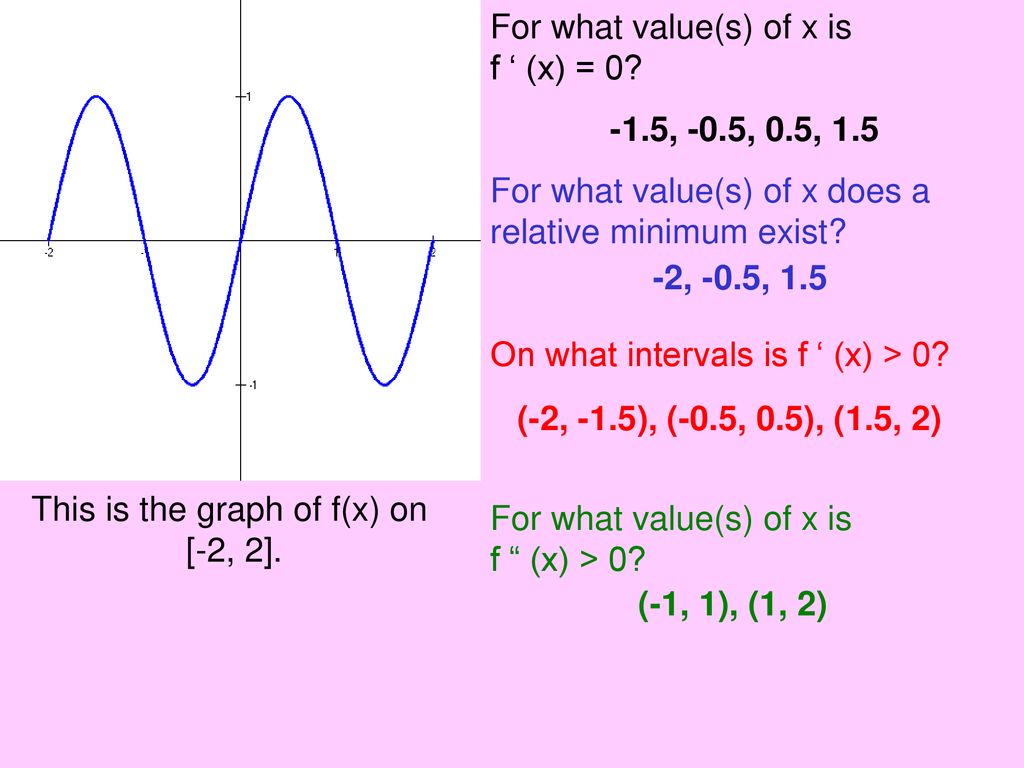



Critical Numbers Relative Maximum And Minimum Points Ppt Download
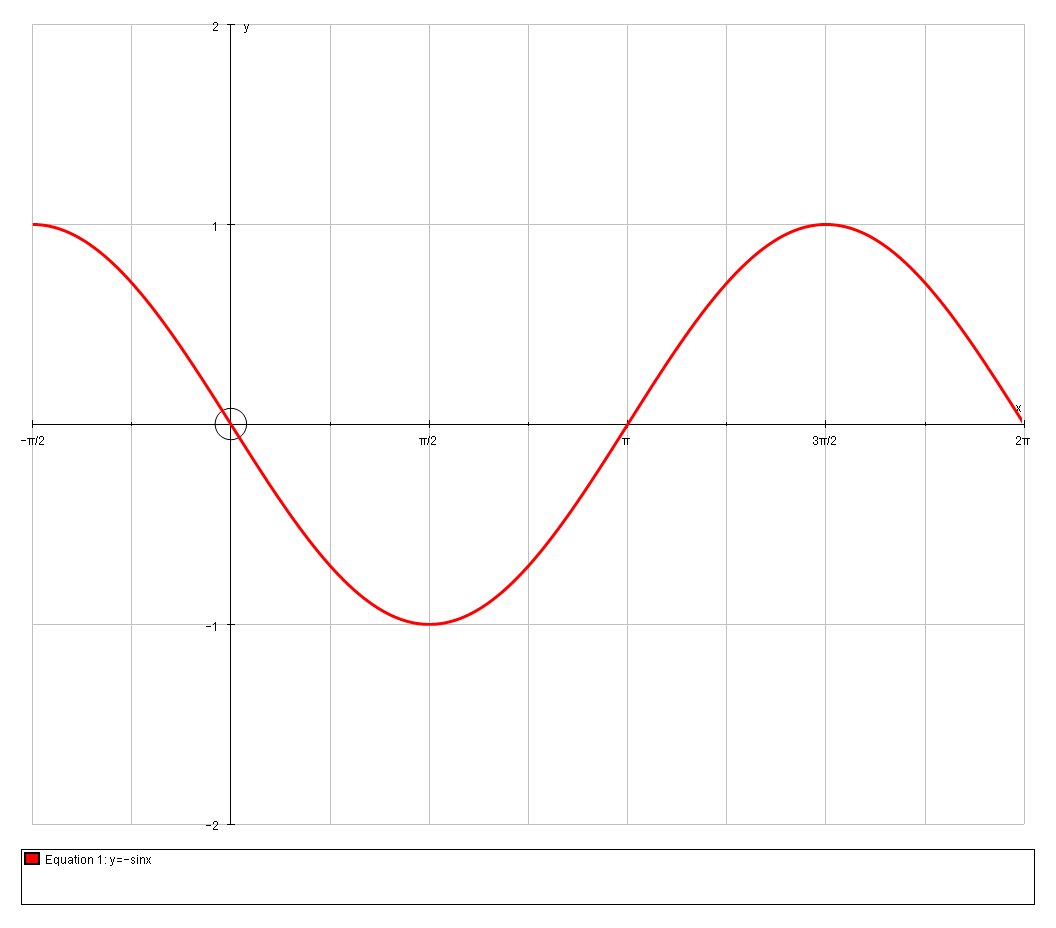



How Do You Graph The Derivative Of F X Cos X Socratic




From The Graph Of The Derivative F X Make A Sketch Of The Original Function F X And Of The Second Derivative F X Mathematics Stack Exchange




Given Fx Sketch The First And Second Derivative Graph Youtube
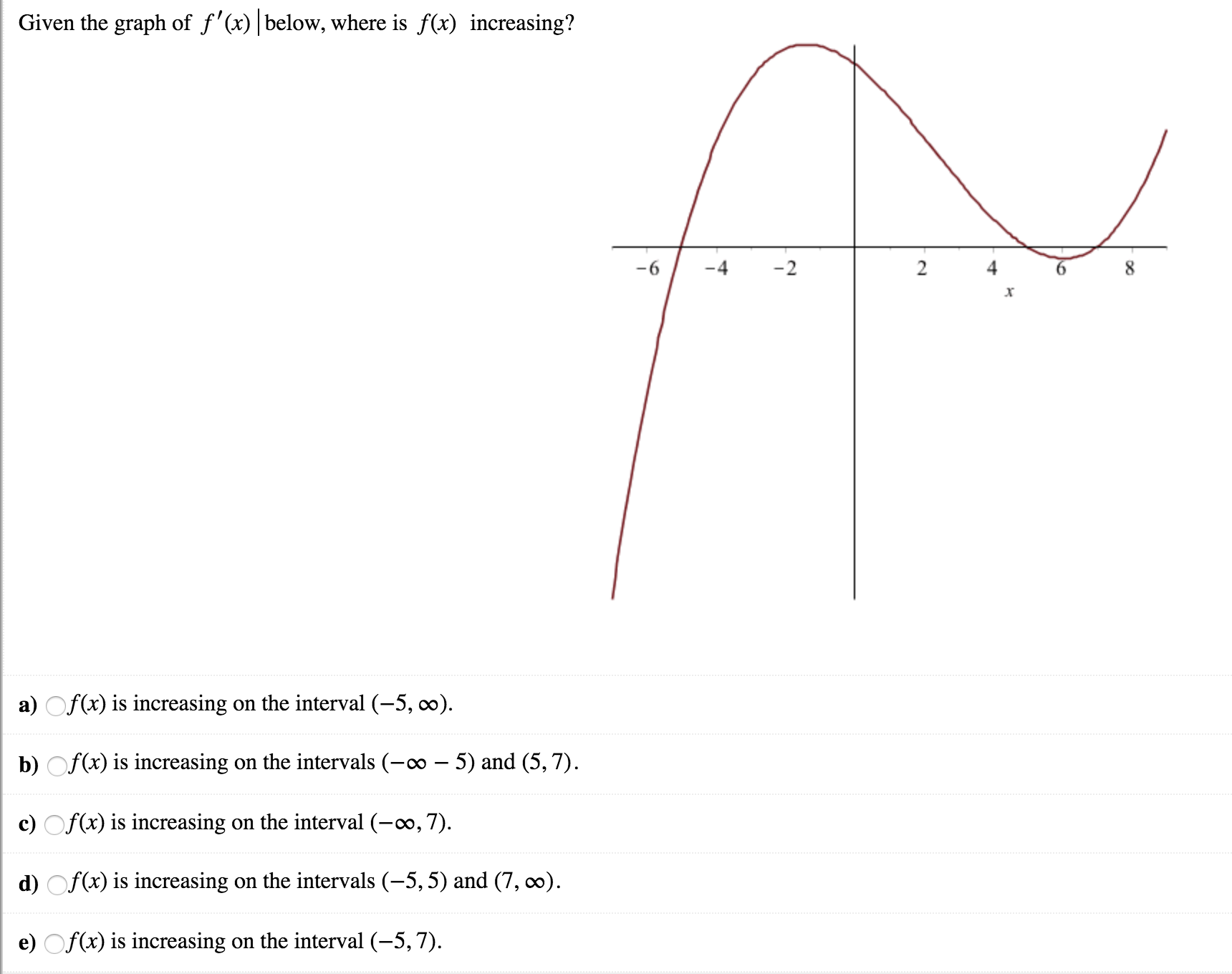



Answered Given The Graph Of F X Below Where Bartleby
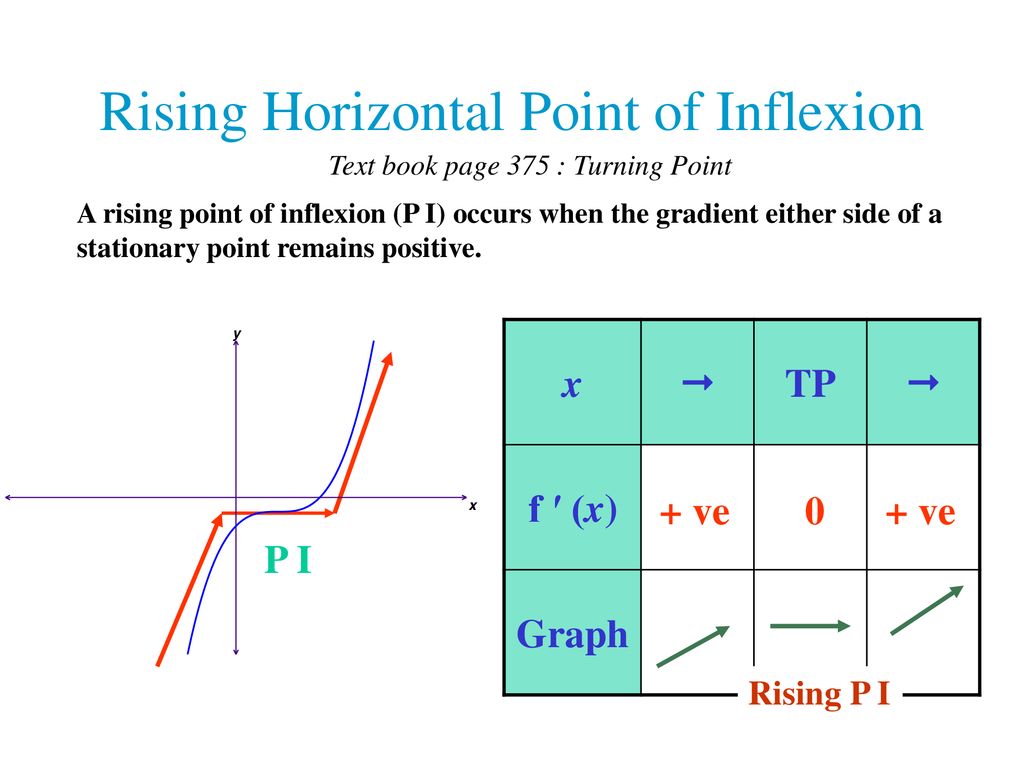



Application Of Differentiation Ppt Download




Reflect Function About Y Axis F X Expii




Ex Determine The Sign Of F X F X And F X Given A Point On A Graph Youtube
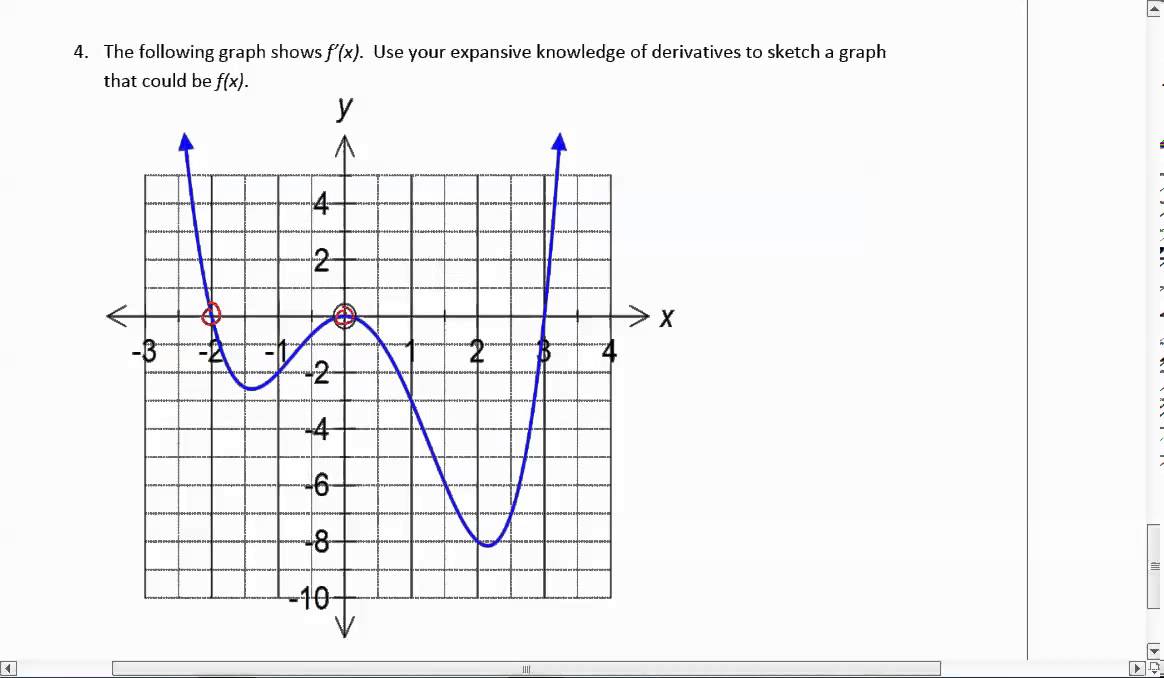



Creating Derivative Graph From The Graph Of F X Youtube
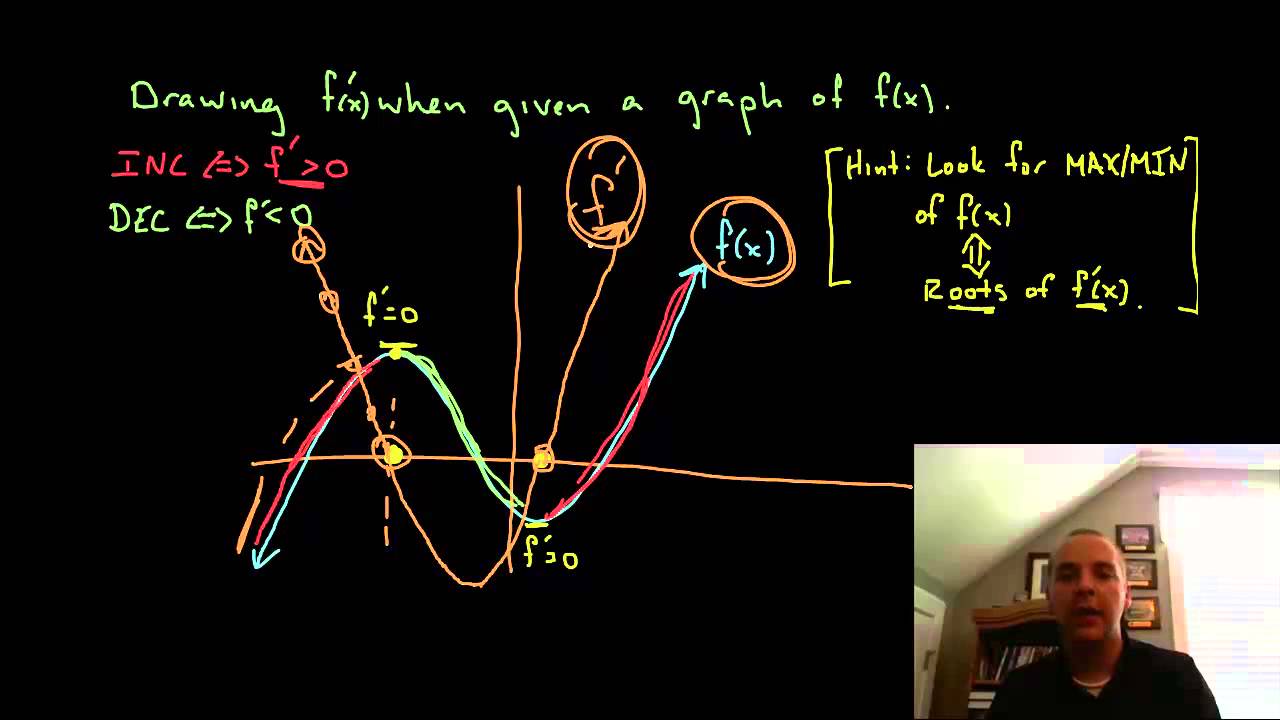



Graphing Derivatives Using Graph Of F X Youtube
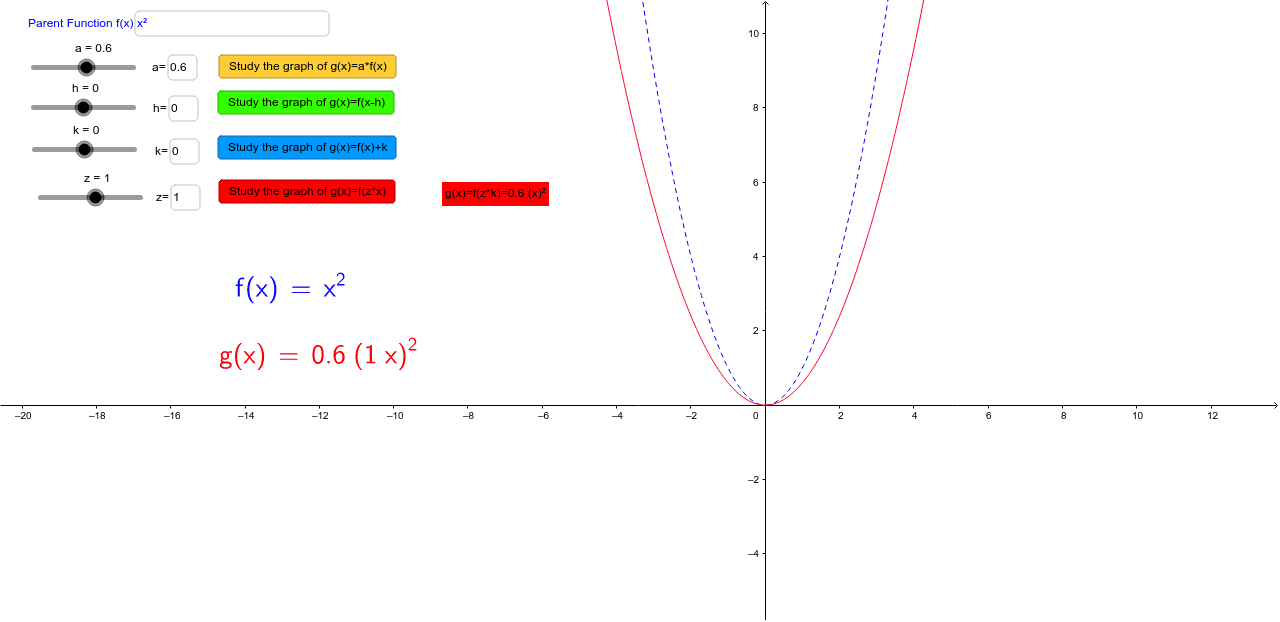



Graph Transformations Discovering Manipulating Functions Geogebra



Answered F X X 4 5x Find F X What Is The Bartleby
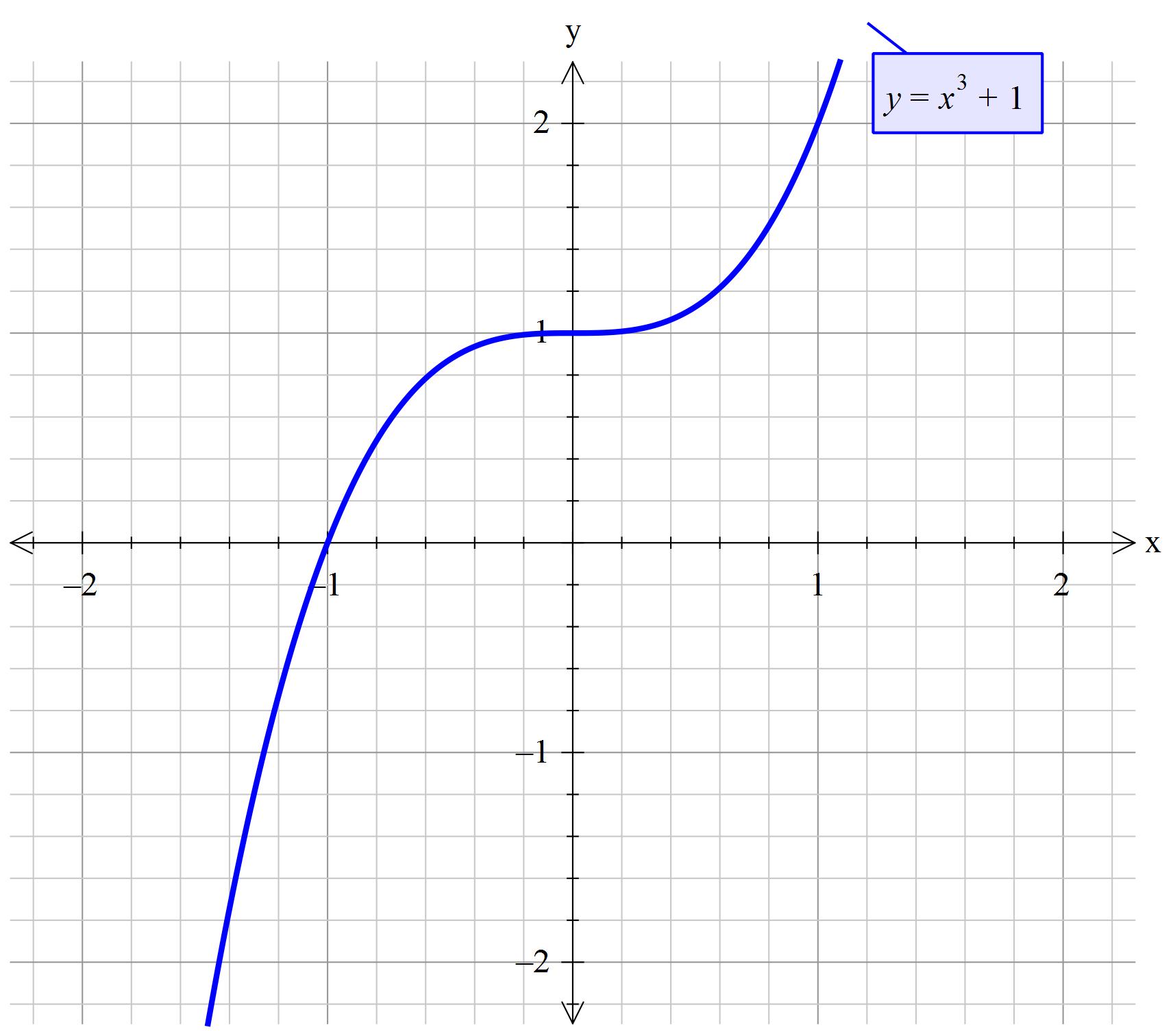



How Do You Sketch The Graph F X X 3 1 Socratic
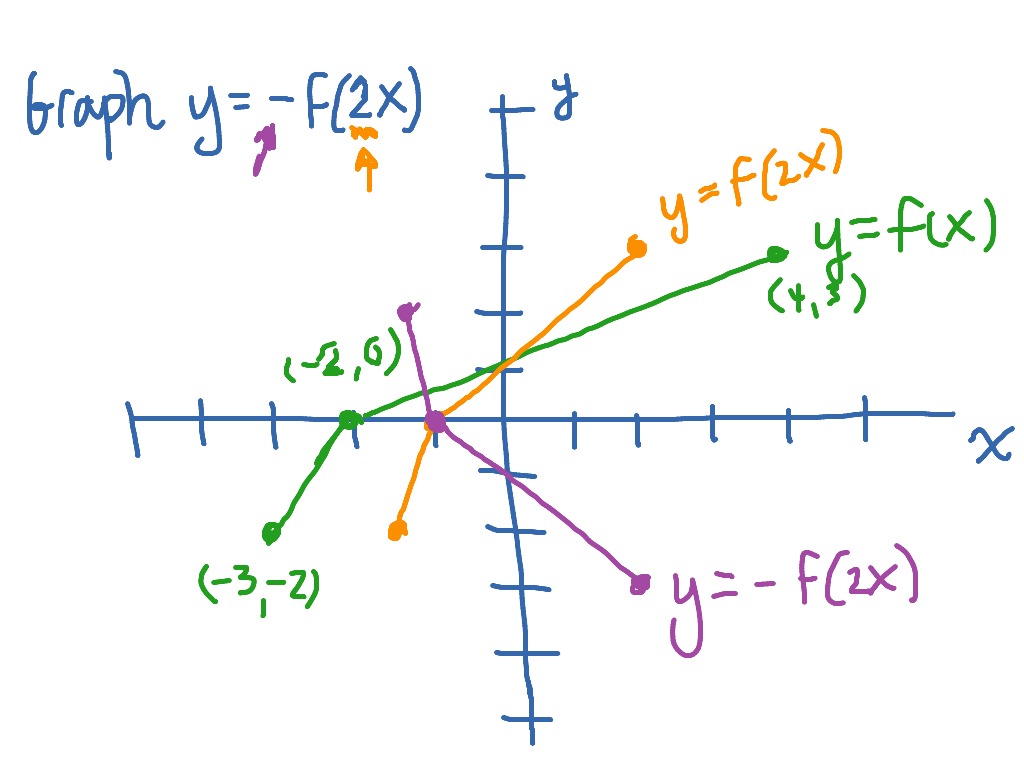



Graphing Y F 2x As A Transformation Of Y F X Math Showme



Numerical Differentiation Wikipedia
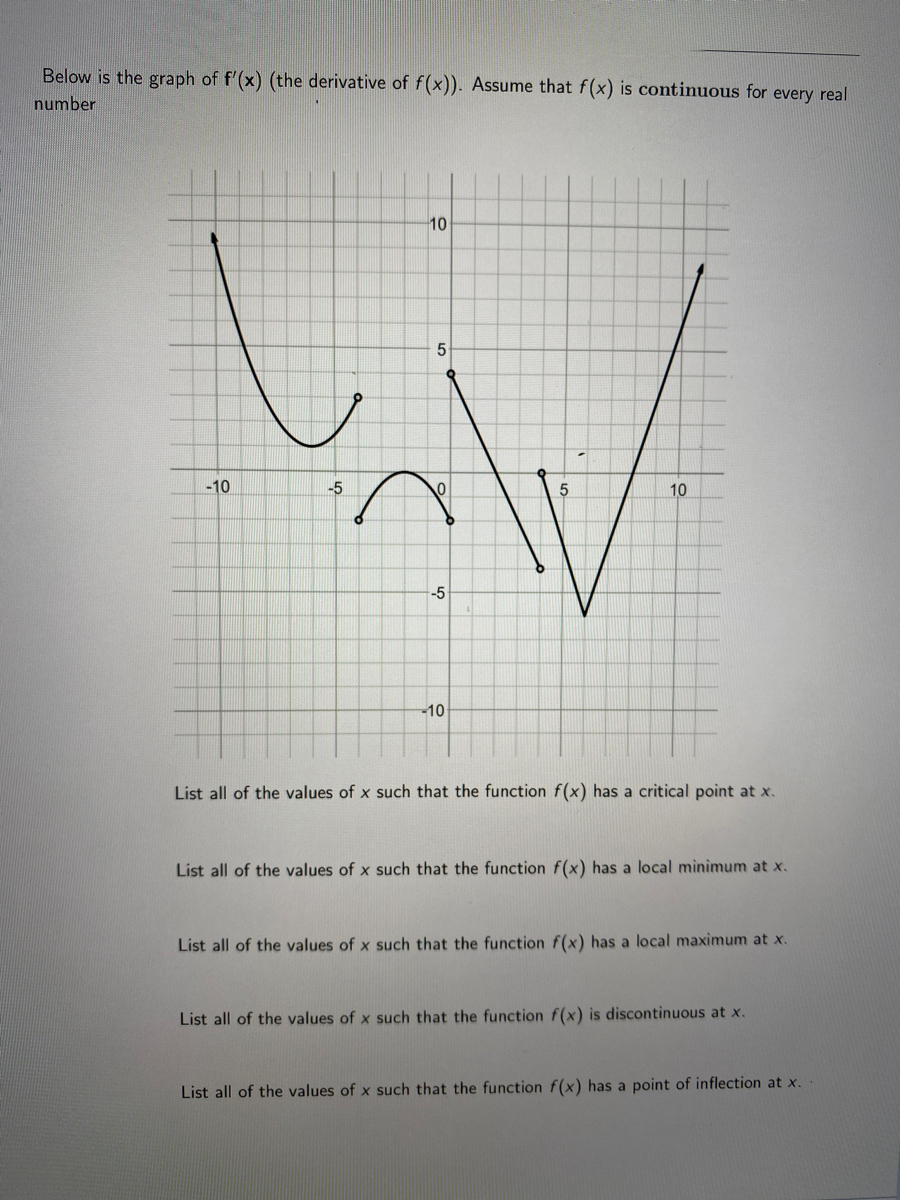



Answered Below Is The Graph Of F X The Bartleby
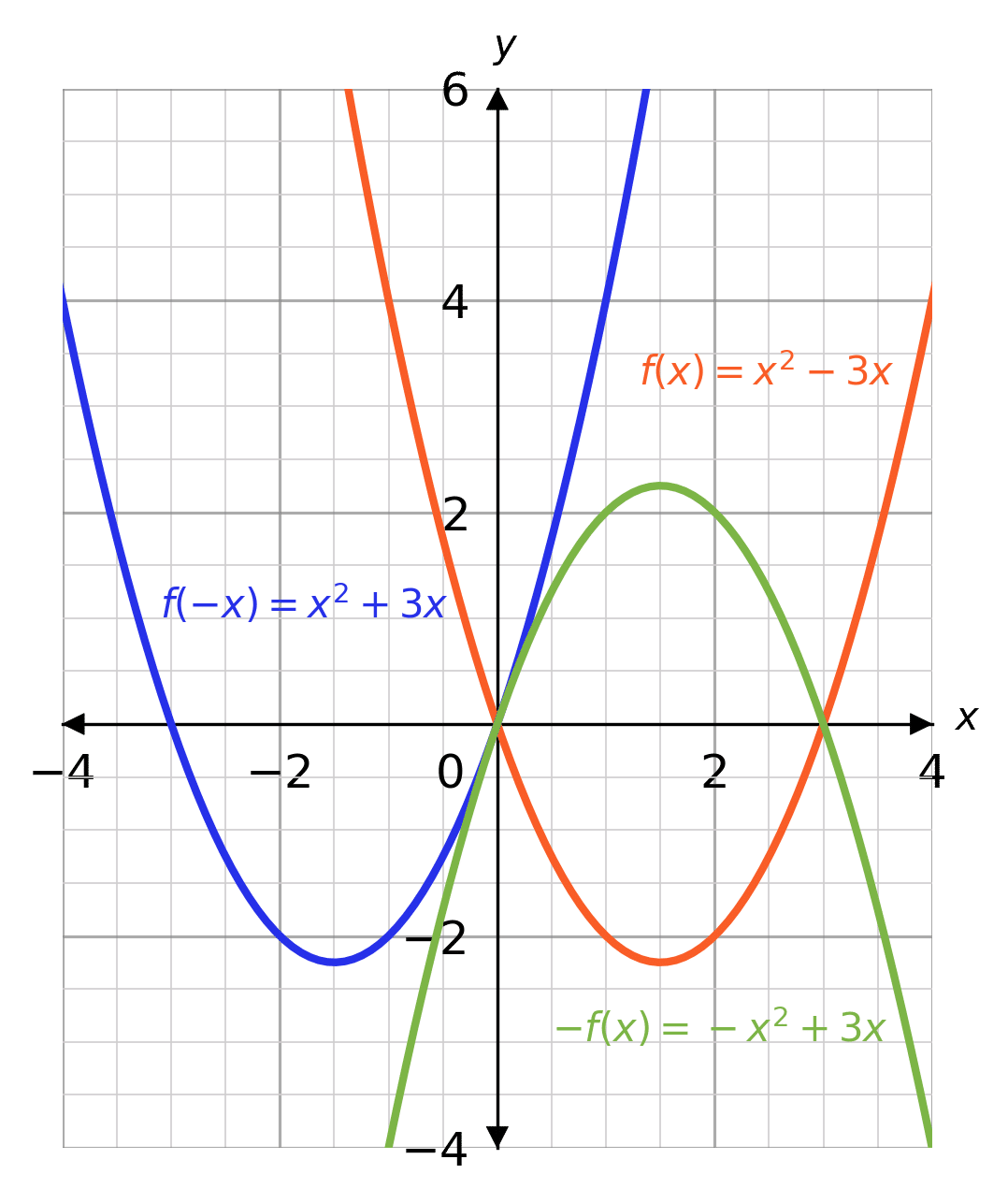



Graph Transformations Worksheets Questions And Revision Mme




Reflecting Compressing Functions Video Khan Academy
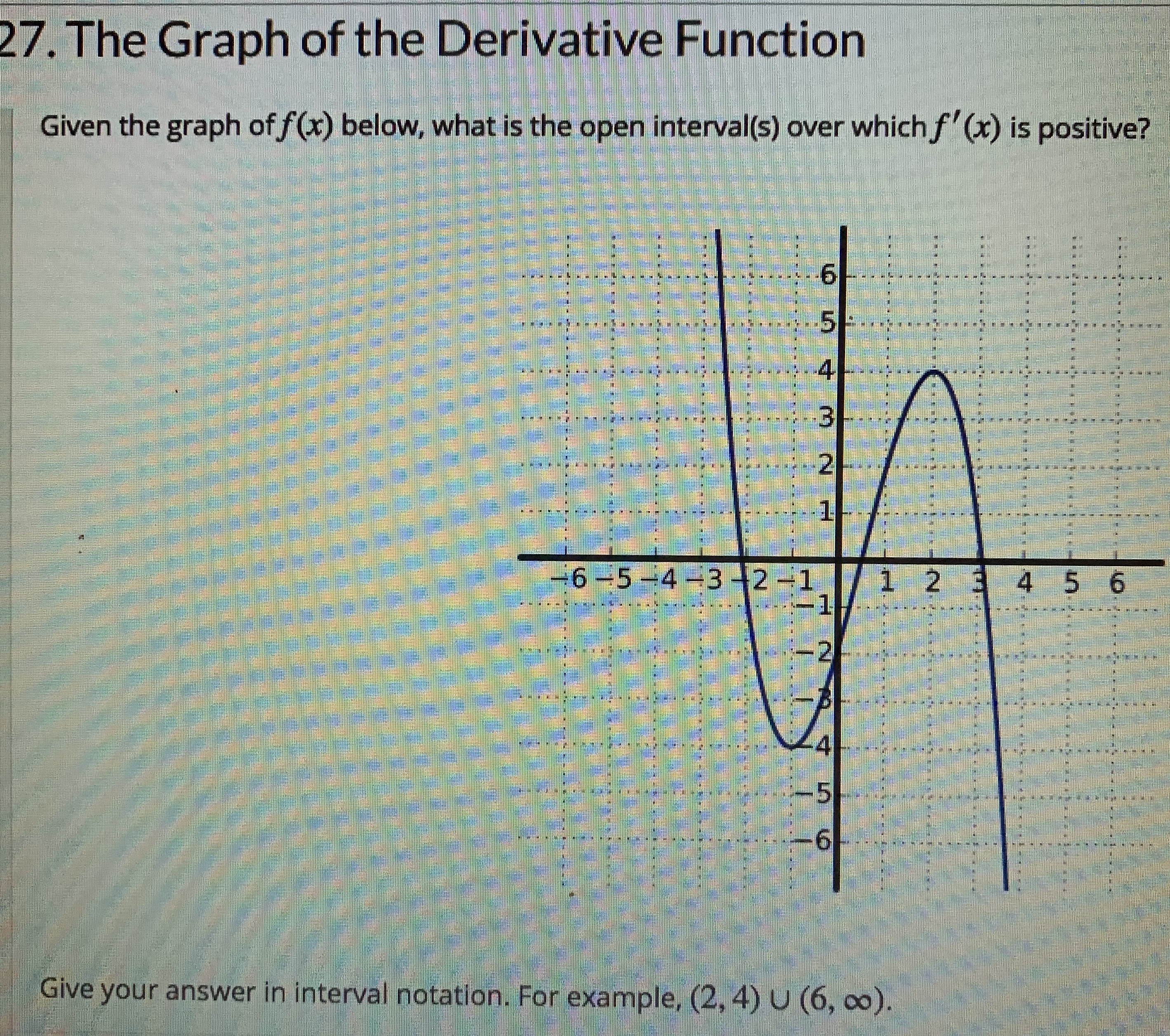



Answered 27 The Graph Of The Derivative Bartleby




Evaluating And Solving Functions College Algebra




The Graph Of F X 3 2 X 3 Is Shown Below G X Is A Transformation Of F X How Would You Write The Brainly Com
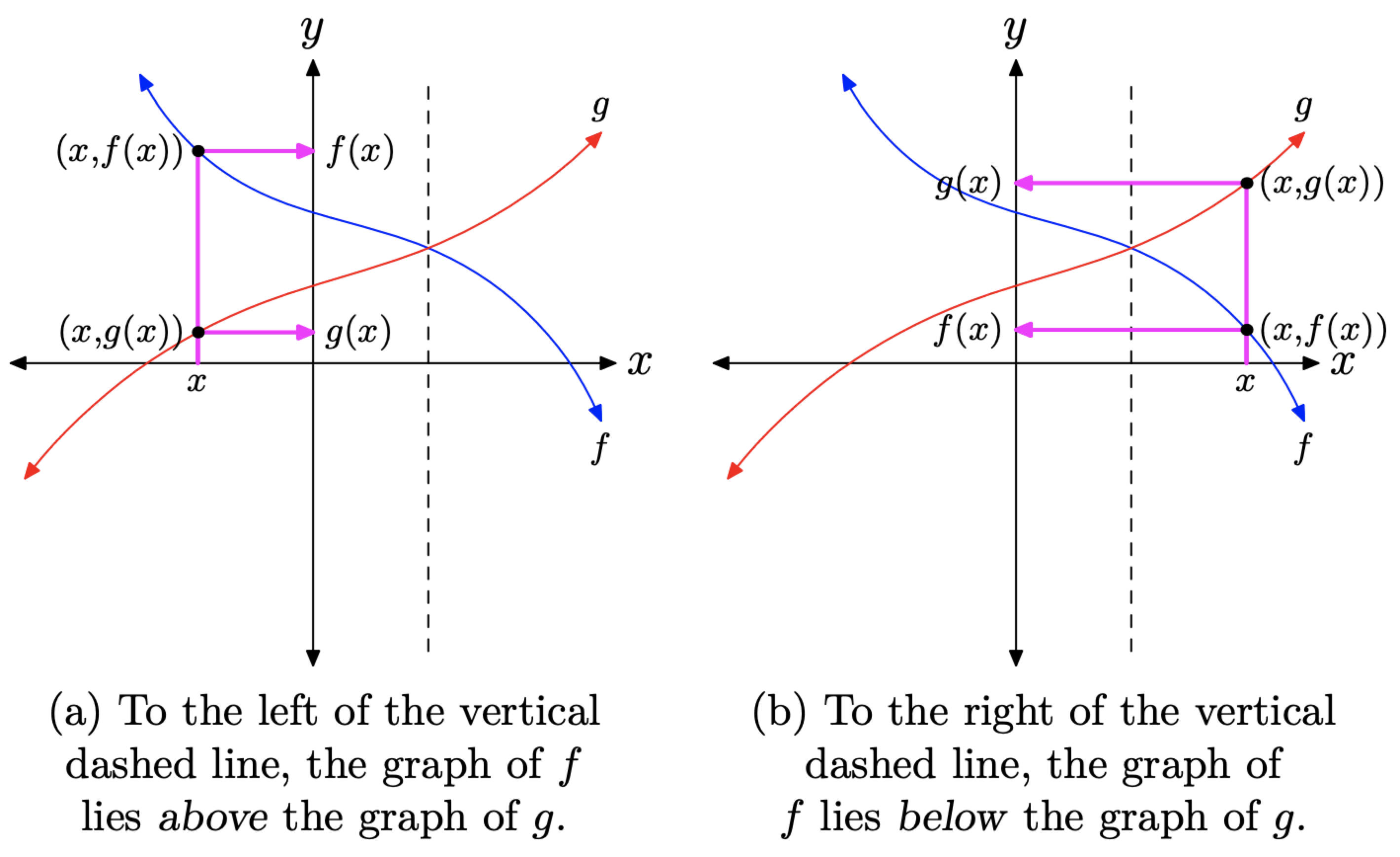



2 4 Solving Equations And Inequalities By Graphing Mathematics Libretexts



No comments:
Post a Comment